Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Community
- Customer Success
- PTC University Training
- Top Down Design - Bearings
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Top Down Design - Bearings
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Top Down Design - Bearings
Using motion skeletons to attempt to completely animate a worm gear. All parts are already modelded top down, and the motion skeleton is complete. Problem is, I cannot figure out how to get the balls and carrier to rotate correctly (rolling along the track). The ratio of turns from the inside to the bearing carrier is a function of the diameters, and figuring out the ratio will be simple, but I'm having trouble on the actual creation of the Skeleton body. If anyone knows how to do this, or knows of a tutorial, it would be great.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's essentially an epicyclic gear.
If the outer race is stationary, and the inner race is rotating (planetary epicyclic: sun in, carrier out, annulus grounded), then the ratio between the inner ring speed and the cage (carrier) speed is [R+1]:1 where R is [outer race contact dia ÷ inner race contact dia].
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The "floating balls" needs a carrier. It is similar to sun gears but you also have a linear component that needs to be programmed into the motion.
Typically people do not show the rotation of the balls but it can be done...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This seems to be what I want to do, but it only shows how to check the links to verify the balls are turning correctly against the carrier. Is there a way to to this with a motion skeleton, or will I be relegated to trying to make it work with mechanism? I don't specifically need the balls to roll, just the carrier and the balls to move. What I think would work is to setup the balls and carrier as their own assembly, then instead of assembling a bearing in, assemble the inner, outer, and carrier/ball pieces. That way (with the motion skeleton), the planes that they are assigned to will rotate independently, and therefore, the inner race and ball/carrier combo will also rotate independently.
The question now is, what is the turn ratio for the carrier itself instead of the bearing's balls.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's essentially an epicyclic gear.
If the outer race is stationary, and the inner race is rotating (planetary epicyclic: sun in, carrier out, annulus grounded), then the ratio between the inner ring speed and the cage (carrier) speed is [R+1]:1 where R is [outer race contact dia ÷ inner race contact dia].
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I hadn't thought to allow the contact diameters as pitch diameters like that, which was a lousy mental excercise on my part. That makes a lot of sense though, and thank you for the help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As a reference, I'll attach an image of the exploded bearing I have thus far.
It's a quick and dirty explode, but it will do the trick. The balls are individual, and patterned around the center axis in the assembly. I'm thinking the Ring carriers, balls, and pins would go into their own assembly, then assign those to another gear pair off the original driving worm. Multiply the reduction from inner race to carrier by the reduction of the original worm. Thoughts?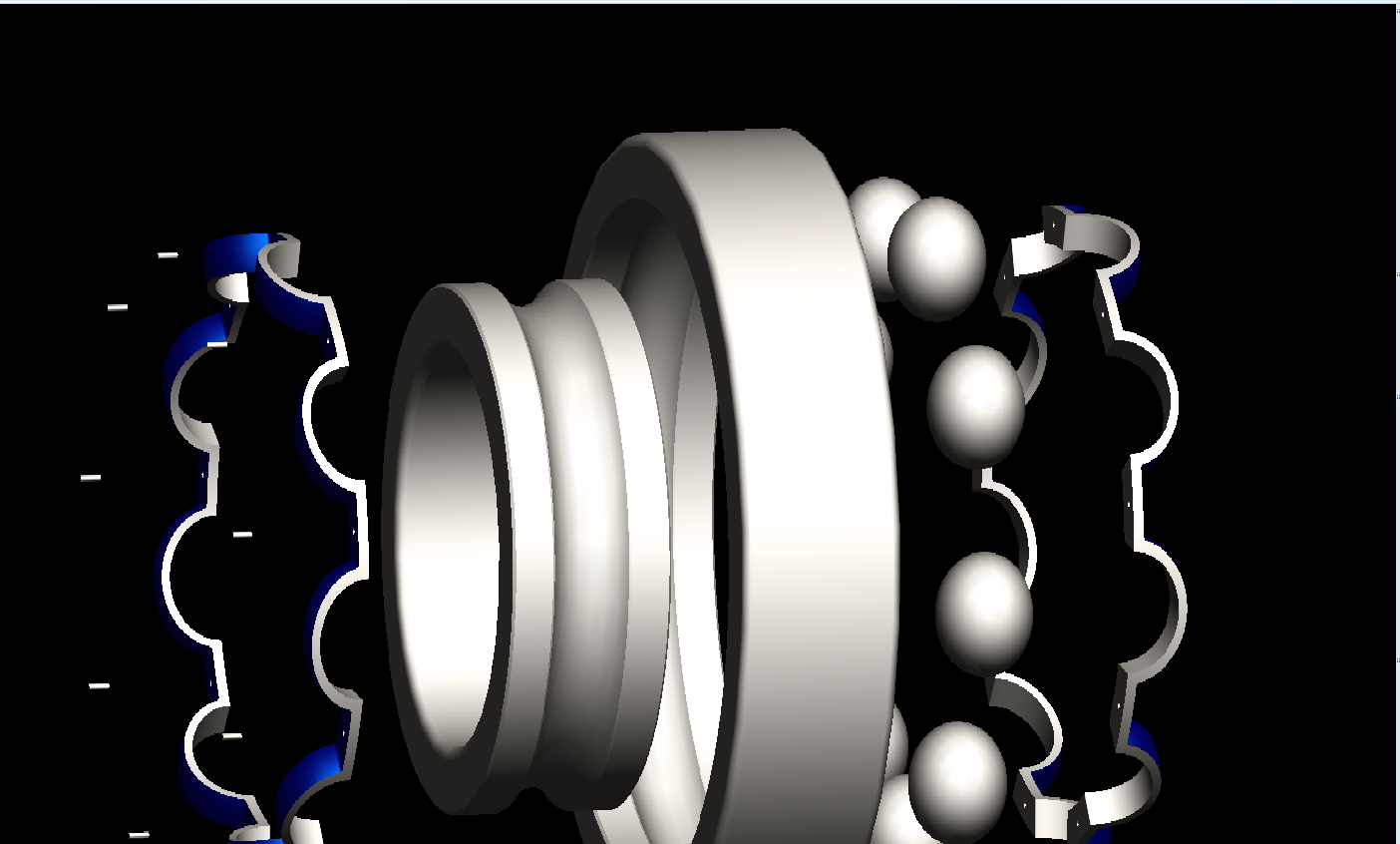
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have done this with planetary gears as well.
This is a great site for calculating this with gear teeth but you can subsitute perimeters (circumference)
http://www.torcbrain.de/uebersetzungsrechner-planetengetriebe/?lang=en
Search Epicycle Gear Calculator in Google will turn up quite a few great links.
In my original bearing, I also did the mental excersize to get it clear in my mind.
Somehow I was thinking you were doing a leadscrew ![]()






