Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathematical ways to draw a heart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathematical ways to draw a heart
Thanks to @mathematicsprof for the reference, here are some fun ways to create a heart using math.
http://www.mathematische-basteleien.de/heart.htm
Can anyone create the three dimensional heart?
-Dan
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cool! The "blue" blood is clearly returning from the body through the right atrium and is being pumped into the right ventricle, where it gets sent out through the pulmonary artery to be re-oxygenated by the lungs.
The "red" oxygenated blood is returning from the lungs into the left atrium,and is being pumped into the left ventricle, where it goes out to the body through the aorta. Or at least that's how I remember it from my college zoology class many years ago. Attached are the Mathcad 13 .xmcd and Adobe .pdf files. I repeat the construction notes here.
Notes on Construction
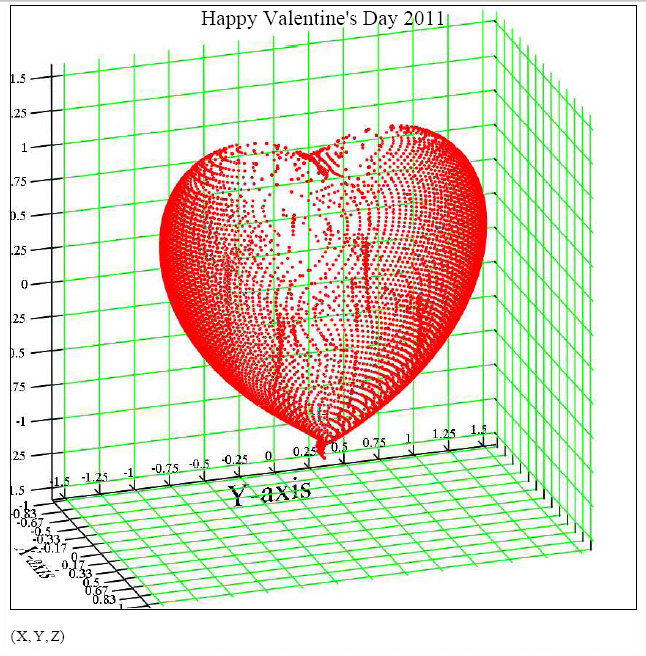
Basic Approach. The basic approach use herein is to calculate values of f = f(x,y,z) with z ranging from -1.5 to 1.5, x ranging from -1 to 1, and y ranging from -1.25 to 1.25. Whenever the absolute value of f is less than a pre-specified tolerance, the y-value is saved and a counter (n) is incremented. When all of the y-values have been computed for a given z and x, then a row of th H matrix, Row = (x,y,z) is saved. The y-value is that y for which | f | is the smallest. This insures that of all the possible y values in an epsilon neighborhood of the true point on the heart's surface, the saved (x,y,z) point is the one closest to the true surface point. The H matrix contains all of the saved surface points; it is an mx3 matrix.
Implicit Function Theorem. The heart surface defines y implicitly as a function of z and x, piecewise in two parts. The first part is the surface piece swept out by an xz plane starting at y = -1.25 and moving to y = -0.5. The second part is the surface piece swept out by the xz plane starting at y = -0.5 and moving to y = 0.0. The implicit function theorem ensures that y is a single-valued function of z and x on each of the two surface pieces. This is why there are two Cor functions, Cor1 and Cor2. Each Cor function is assured of finding at most exactly one y on or near the heart surface as y sweeps to the right along each of the two surface pieces.
Bilateral Symmetry. Cor1 and Cor2 only construct the left half of the heart. The right half is, and must be obtained by invoking the bilateral symmetry of the heart, because y would not be a function of z and x if we swept from y = -1.25 all the way to y = +1.25. Given the mx3 matrix H-left that describes the left side of the heart, H-right is just H-left with the second column, the column of y values, multiplied by -1.
A Final Note
Dan's reference actually shows two three-dimensional heart figures. I chose to work with the on on the right. I can see now that the one on the left would have been easier to work with. In that figure, the heart is sliced into two surfaces by the xz plane. On the upper and lower surfaces, y is implicitly a single-valued function of x and z. These upper and lower surfaces do not need to be further subdivided in order to have single-valued functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dan,
Yes. Here is a screen shot. I'll post the Mathcad 13 .xmcd and .pdf worksheet files tomorrow.
Roger Mansfield
P.S. The figure is a 3D scatter plot. I took the equation for the surface from the reference that you provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cool! The "blue" blood is clearly returning from the body through the right atrium and is being pumped into the right ventricle, where it gets sent out through the pulmonary artery to be re-oxygenated by the lungs.
The "red" oxygenated blood is returning from the lungs into the left atrium,and is being pumped into the left ventricle, where it goes out to the body through the aorta. Or at least that's how I remember it from my college zoology class many years ago. Attached are the Mathcad 13 .xmcd and Adobe .pdf files. I repeat the construction notes here.
Notes on Construction
Basic Approach. The basic approach use herein is to calculate values of f = f(x,y,z) with z ranging from -1.5 to 1.5, x ranging from -1 to 1, and y ranging from -1.25 to 1.25. Whenever the absolute value of f is less than a pre-specified tolerance, the y-value is saved and a counter (n) is incremented. When all of the y-values have been computed for a given z and x, then a row of th H matrix, Row = (x,y,z) is saved. The y-value is that y for which | f | is the smallest. This insures that of all the possible y values in an epsilon neighborhood of the true point on the heart's surface, the saved (x,y,z) point is the one closest to the true surface point. The H matrix contains all of the saved surface points; it is an mx3 matrix.
Implicit Function Theorem. The heart surface defines y implicitly as a function of z and x, piecewise in two parts. The first part is the surface piece swept out by an xz plane starting at y = -1.25 and moving to y = -0.5. The second part is the surface piece swept out by the xz plane starting at y = -0.5 and moving to y = 0.0. The implicit function theorem ensures that y is a single-valued function of z and x on each of the two surface pieces. This is why there are two Cor functions, Cor1 and Cor2. Each Cor function is assured of finding at most exactly one y on or near the heart surface as y sweeps to the right along each of the two surface pieces.
Bilateral Symmetry. Cor1 and Cor2 only construct the left half of the heart. The right half is, and must be obtained by invoking the bilateral symmetry of the heart, because y would not be a function of z and x if we swept from y = -1.25 all the way to y = +1.25. Given the mx3 matrix H-left that describes the left side of the heart, H-right is just H-left with the second column, the column of y values, multiplied by -1.
A Final Note
Dan's reference actually shows two three-dimensional heart figures. I chose to work with the on on the right. I can see now that the one on the left would have been easier to work with. In that figure, the heart is sliced into two surfaces by the xz plane. On the upper and lower surfaces, y is implicitly a single-valued function of x and z. These upper and lower surfaces do not need to be further subdivided in order to have single-valued functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You two sure went above and beyond the call. Thank you for sharing the video and supplementary worksheets.AWESOME
-Dan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nicely done. I have not messed around with 3D plots before, so I will study this one.
Thanks,
Wayne
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In following up on the final note of my previous post, I found that using the second equation of the Reference web page (in the "Threedimensional" heart section) leads to a shorter, much faster worksheet. I have attached the .xmcd and .pdf files for this improved version.
The attached .xmcd worksheet is shorter and faster because it only needs one Cor function, vs. Cor1 and Cor2 in the earlier worksheet. Also, it invokes front-to-back as well as bilateral (side-to-side) symmetry to construct the heart surface, whereas the earlier worksheet only invokes bilateral symmetry.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator





