Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Re: Need to build repetitive curve in a sketch
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Need to build repetitive curve in a sketch
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Need to build repetitive curve in a sketch
I am needing to build a sketch that the curve needs to follow an exact pattern. I have attached a sketch that shows the basic curvature. (As it is freehand the shape is not exact however)
The pattern of curvature needs to follow a point placement like this. The initial point is at X=0 and Y=+.06. The second point on the curve would be X=+.5 and Y=-.06. The 3rd point on the curve would be X=1 and Y=.06. Etc...
I want to build a curve where I don't have to manually enter the dimensions as the size will extend for close to 50 inches.
My initial thought would be that Relations might be the way to go, but I have no experience with this and don't know if it would be capable of what I am looking to do.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
X= 40*(t*720)
Y= 4*sin*(t*360)
Z=0
In this case 40 is the wavelength.
720 is 2 cycles
I think 4 is amplitude for y
Z is zero because it's in a single plane.
Difficult when not in front of a car screen to check.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Still looking this over online. I haven't pieced this together but I am now wondering whether this can be done as a relation at all within a sketch.
I am seeing examples how using a variable section sweep can influence different shapes but haven't seen a simple straight line oscillating curve that would result in the basic sweep shape of the curve on my initial post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
HI, Use curve from equation.
Datum\Curve\curve from equation. Example can be tailored from below.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Rcrerar-2: The images you attached aren't showing. I will see if I can find the location you are suggesting but if there is an easy way to see these images it would be great.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
X= 40*(t*720)
Y= 4*sin*(t*360)
Z=0
In this case 40 is the wavelength.
720 is 2 cycles
I think 4 is amplitude for y
Z is zero because it's in a single plane.
Difficult when not in front of a car screen to check.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is excellent!
I just did find a video that showed roughly what I needed and proved this out.
I will check to see how your numbers differentiate.
This is a little fudgy so it may be that your numbers are closer in line than the formula I was using.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
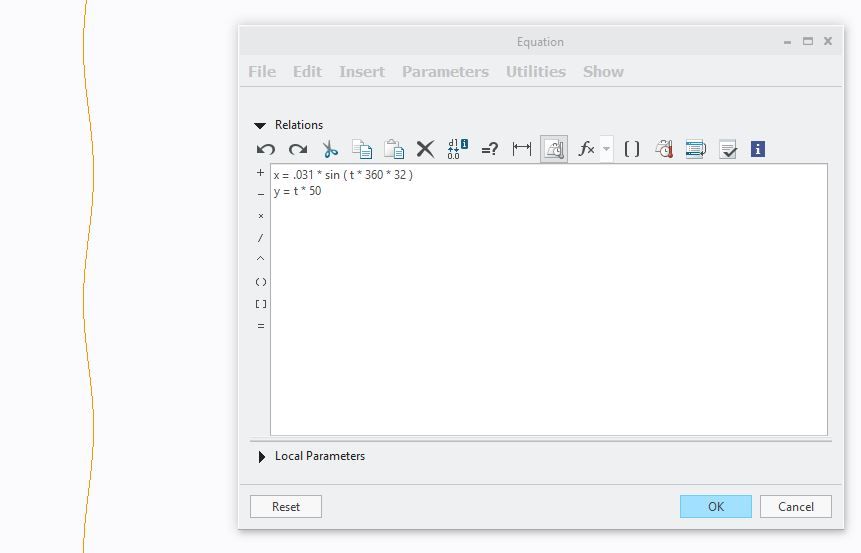
Just Checked the formula I used.
x=50*t
y= 4*sin(t*720)
z=0
curve would be 50 units long and total height is 8 units crest to crest. This produces 2 cycles if you want more then each cycle is multiple of 360.
If it is not a sin curve then the maths needs working out.
Have fun.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Subsitute 'sin' for 'cos' in the formula & you get another variation of the curve.
Worth a mention.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
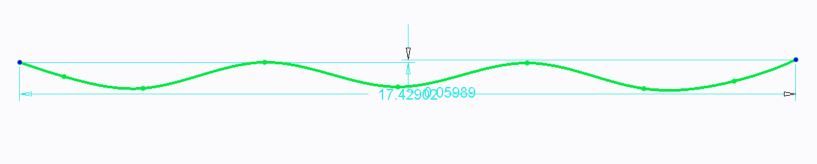
rcrerar: Here is the formula that I went with. This worked great.
I will be able to use this pattern in the straight stretches, but unfortunately I can not use this for twisting around a large radii in our die. With that I will be developing a different technique involving a pattern and some fillets.
When you extrude this feature it looks a lot like a sun chip. Unfortunately I can't bend this feature at a specific large radii while maintaining the tilt I will need.
John: I did for a while consider the cosine function for doing a bend, but in the end I knew it would be a bear to maintain a specific bend radii as well being unable to carry through the proper inclination.
In the end I know that I can still use this for the straight stretches in my die. It gives a beautiful result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"I will be able to use this pattern in the straight stretches, but unfortunately I can not use this for twisting around a large radii in our die. With that I will be developing a different technique involving a pattern and some fillets."
I am not sure what you mean exactly by your statement but would the attached image help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John: Your example does place the general inclination of the curvature we are after. Unfortunately the inclination needed is not 90 degrees as in your example, but 72 degrees. The long linear portion that we would use gets tilted that amount through the tilted CSYS.