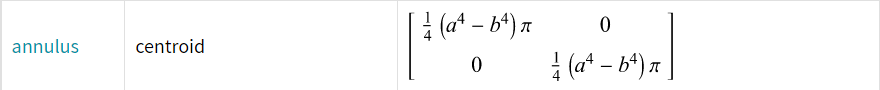Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Community
- Creo+ and Creo Parametric
- Analysis
- Finding second area moment of inertia over a chang...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Finding second area moment of inertia over a changing cross section
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finding second area moment of inertia over a changing cross section
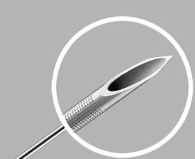
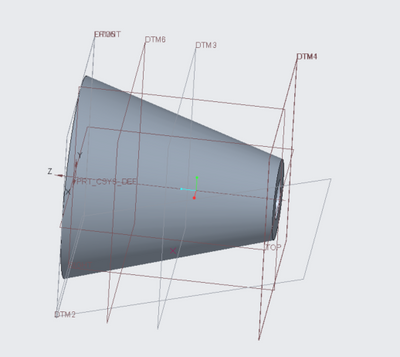
Hello! I was wondering about Creo’s capability to measure the Second Area Moment of Inertia (I). I am trying to calculate the second area moment for a common vascular needle, which has a cylindrical shaft and a conical tip. I was mostly wondering if Creo is able to find the second area moment over the varying geometry of the conical tip, or if it is only able to find one cross section at a time. I have attached a picture of what the needle end looks like below. I believe this process would require me to integrate by hand, as well as utilize the parallel axis theorem to connect the conical end of the needle to the cylindrical shaft. I thought Creo may have some functionality to do this within the program. Please let me know if I can clarify my problem in any way. It seems like Creo has lots of capabilities to find the mass properties of different parts, but since I need the area moment of inertia the mass properties are not required and instead geometry is my biggest concern.
Thank you,
Adam
Solved! Go to Solution.
- Labels:
-
General
-
Mechanism Design
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I now understand.
My suggestion above to use BMX is still valid to automate this process. Use a field point on the bias cut and the central axis to move the section plane along the central axis and plot the results. If you do not have the BMX module, then you can do this manually by plotting the results from each cross section. You will not need too many points to get an accurate curve in this case.
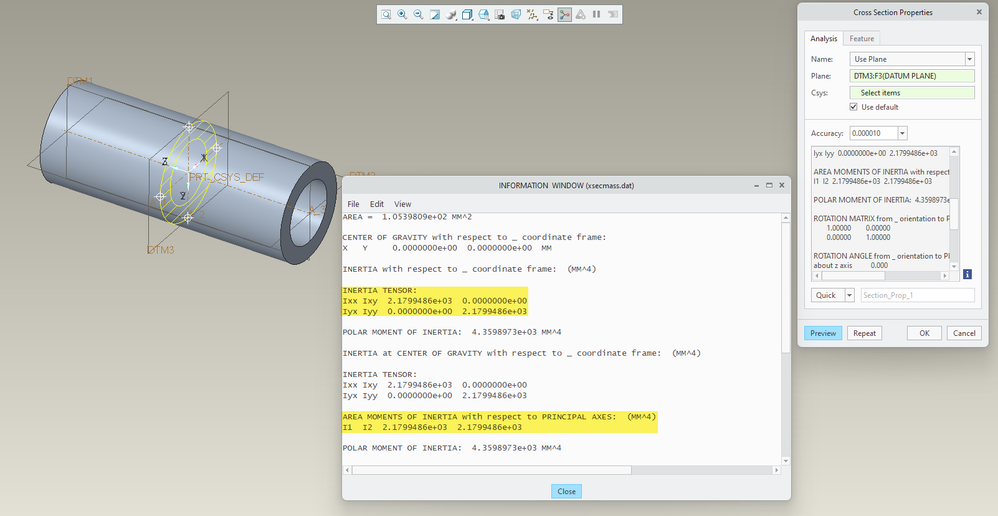
Creo will report the value for I at any arbitrary section. The measure of interest is found as @StephenW has already mentioned. Within the results the inertia tensors are presented as shown below. You should do manual calculations for verification but generally Creo should be very accurate on these results.
Derived tensor for area moment of inertia of an annulus wrt to centroid:
Involute Development, LLC
Consulting Engineers
Specialists in Creo Parametric
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is not clear exactly what you are trying to do. Do you need the resistance to bending of the tube with a bias cut on the end? The SI units for moment of inertia are Kg m^2 so it is a 2D calculation. To extrapolate to 3D you would use the mass moment of inertia.
Would the value of I (Kgm^2) with respect to the neutral axis of bending with an assumed loading condition give you what you need?
I am assuming that you are interested in the moment of inertia of circular tube with respect to any axis passing through its centroid which is a constant value if the tube wall is a constant. It only changes at the bias cut forming the point of the needle.
Creo can in theory measure "I" at any cross section with a closed area. Using the Creo BMX extension, you can take the cross section at a specific point. With BMX there is a special type of datum point (a field point) that will support automating finding the min/max value within a specified domain automatically. You can plot these values as well in BMX. You could have Creo calculate "I" at discrete steps and plot the value as a function of the distance along the central axis of the tube. The only domain of interest in this case would be where the bias cut is made on the tube as "I" will decrease from the constant value of the tube to zero at the point. If you plot "I" as a function of position along the central axis, then you have used numerical methods in Creo to do the Calculus.
Involute Development, LLC
Consulting Engineers
Specialists in Creo Parametric
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello! I am trying to find the area moment of inertia (m^4), I was wondering if there is a way to do this in Creo. It seems like most of the time you have to incorporate mass, but I am hoping to find area moment of inertia instead of the usually calculated mass moment of inertia. I am hoping to use this equation along with Euler's formula to estimate the buckling force in the needle, similar to the cross section of a beam.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
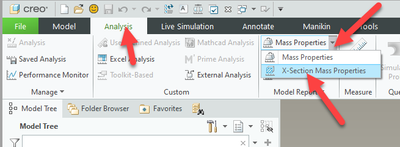
Under the analysis tab, Mass Properties has a drop down that lets you select x-section mass properties and will generate the area moment of inertia.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello! Will it do this accurately even if the cross section is not consistent across the part?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would guess that Creo can accurately calculate the value at any given section. If you are concerned, take a few simple examples that can be hand calculated and verify.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I now understand.
My suggestion above to use BMX is still valid to automate this process. Use a field point on the bias cut and the central axis to move the section plane along the central axis and plot the results. If you do not have the BMX module, then you can do this manually by plotting the results from each cross section. You will not need too many points to get an accurate curve in this case.
Creo will report the value for I at any arbitrary section. The measure of interest is found as @StephenW has already mentioned. Within the results the inertia tensors are presented as shown below. You should do manual calculations for verification but generally Creo should be very accurate on these results.
Derived tensor for area moment of inertia of an annulus wrt to centroid:
Involute Development, LLC
Consulting Engineers
Specialists in Creo Parametric
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
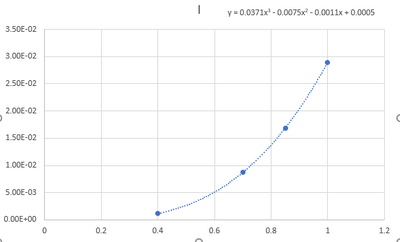
I began plotting the moments of inertia along the conical end of the needle. It looks like when plotting these points there is a polynomial distribution along the needle tip (a picture of the part and the I-value distributions are shown below). Would finding the area under this curve yield the estimated area moment of inertia for the entire part? I just wanted to make sure I clarified that I have been interpreting the data properly. I appreciate all your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With the values of I along the length of the beam, you should be able create a bending moment/shear diagram. That will give you a graphical representation of what is happening with a bending load. Is that not the data you need?
Involute Development, LLC
Consulting Engineers
Specialists in Creo Parametric
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just need the area moment of inertia over the entire body so that I can use Euler's equations to find the buckling force. However, I believe finding the area under this graph should suffice for this right?