- Community
- Creo+ and Creo Parametric
- Analysis
- Force Measures on Spring Groups
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Force Measures on Spring Groups
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Force Measures on Spring Groups
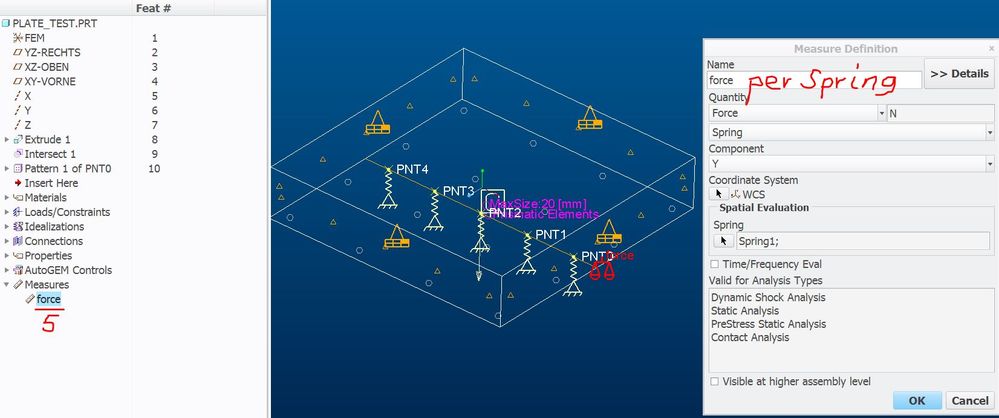
Springs are very useful in place of constraints to better simulate a boundary condition. Spring Force (Mag, or X,Y,Z) Measures can be created for Pt-to-Grnd springs to report the reaction at the spring. I created some spring groups by using both patterned points and by selecting multiple points. A subsequent Measure created for the springs in the group only allows selection of the group, and returns one value. The resulting value was not as expected. One would expect that a Measure on a Spring Group would be the Net of the group. It was not. Neither was it the average of the springs in the group. I don't know what the number was. Has anyone tried this, and found usable results?
Solved! Go to Solution.
- Labels:
-
Simulate
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is what it is doing...
The force measure on a "group of springs" comes as the largest magnitude of any ONE of the springs in the group.
Two ways to correctly sum the spring forces
- create individual springs and a measure for each spring separately. (cannot use pattern)
- create displacement measures (Y) at each point in the group (can use pattern) Then convert to force by hooks law. For a pattern it will automatically create the correct number of displacement measures with the point name at the end like PNT0, PNT1... automatically added in example below.
Since your stiffness is 1 N/mm and the displacements mm then these are in N already.
You could create "computed" measures to do the conversion if desired.
note corners 1 and 3 are a spring group and 0 and 2 are another.
See how the result with the maximum absolute value is reported for each group:
Displ_PNT0: -2.633724e+00
Displ_PNT1: -2.049987e+00
Displ_PNT2: -1.466250e+00
Displ_PNT3: -8.825128e-01
Displ_PNT4: -2.987757e-01
Displ_corner_0: -4.793563e+00
Displ_corner_1: -1.057623e+00
Displ_corner_2: -1.874877e+00
Displ_corner_3: 1.861063e+00
s1force: -2.633724e+00 (pattern of 5 points)
s2force: 4.793563e+00 (corner 0 and corner 2)
s3force: 1.861063e+00 (corner 1 and corner 3)
13.0N applied
19.6 grams * 1 g = 0.2N
Total is 13.2N
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, if I understand well, for example, you have a surface (meshed with solid elements) that normally is constrained in XYZ with a "normal constraint command". In this way, however, this surface will be treated like a rigid one. In addiction this normal constraint doesn't permit the nodes rotation that occours with the deformation of the support surface.
If what you want to do is putting N-points over the surface (eg: a pattern of ones) and "constraint" each one with a spring, then you have to build N springs. But in this way, in addiction of a lot of work, you will have N areas of stress concentration.
Maybe a work-around could be creating a weighted link between the surface and an external point, then by constrainig this last one with a ground spring with high values in both traslation and rotation degrees. In fact weighted links allow the surface deformation.
More infos here.
Bye
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure you understood my question. I do not have any issues with figuring out the correct way to apply boundary conditions, in this case I want springs for a very specific reason. The question is about Measures on Springs, specifically groups of springs. The results of the measure I created are wrong, or, I misunderstand just exactly what a Spring Force measure is reporting. Put simply, though...the net of all spring forces should equal the net of all external loads when springs are the only constraint. They didn't.
Gavin
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
skunks,
Thank you for the additional model...however, it suffers from the same symmetry conditions so as to not totally validate the measure responses.
I have added some features to your test plate model...see attached. The results are:
Resultant Load on Model:
in global Y direction: -1.319625e+01
...now with 3 rows of springs, an off-center load, and no edge constraints.
s1force: -2.633724e+00 (1 spring "feature" w/5 springs)
s2force: 4.793563e+00 (1 spring "feature" w/2 springs)
s3force: 1.861063e+00 (1 spring "feature" w/2 springs)
I submit that you cannot combine these in any way to achieve the net (compression) equal to the external load of -13.196.
Gavin
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is what it is doing...
The force measure on a "group of springs" comes as the largest magnitude of any ONE of the springs in the group.
Two ways to correctly sum the spring forces
- create individual springs and a measure for each spring separately. (cannot use pattern)
- create displacement measures (Y) at each point in the group (can use pattern) Then convert to force by hooks law. For a pattern it will automatically create the correct number of displacement measures with the point name at the end like PNT0, PNT1... automatically added in example below.
Since your stiffness is 1 N/mm and the displacements mm then these are in N already.
You could create "computed" measures to do the conversion if desired.
note corners 1 and 3 are a spring group and 0 and 2 are another.
See how the result with the maximum absolute value is reported for each group:
Displ_PNT0: -2.633724e+00
Displ_PNT1: -2.049987e+00
Displ_PNT2: -1.466250e+00
Displ_PNT3: -8.825128e-01
Displ_PNT4: -2.987757e-01
Displ_corner_0: -4.793563e+00
Displ_corner_1: -1.057623e+00
Displ_corner_2: -1.874877e+00
Displ_corner_3: 1.861063e+00
s1force: -2.633724e+00 (pattern of 5 points)
s2force: 4.793563e+00 (corner 0 and corner 2)
s3force: 1.861063e+00 (corner 1 and corner 3)
13.0N applied
19.6 grams * 1 g = 0.2N
Total is 13.2N
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Resultant Load on Model:
in global Y direction: -1.925213e+00
Then, your Measure returns
force4: -4.813031e-01
...which is exactly 1/4 of the total load. So, does the measure just arbitrarily pick one spring to report the spring for from it? Which one? Or, is it an average of the 4? It certainly is not the net. Try moving the load to a non-symmetrical location.
Gavin
Maybe, it behaves similar to Loads in the first place and so when four locations are picked to create the "spring", it actually divides the properties out over all four locations?