We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Community
- Creo+ and Creo Parametric
- Customization
- Re: Christmas challenge...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Christmas challenge...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Christmas challenge...
Hi simulation geeks out there... In case you get bored during the holidays, I thought I'd challenge you with an optimization task...
This is a simulation task that was inspired by a failed vacation project that I undertook a few years ago with my then 8 year old stepson.
I want to design and optimize an archery bow that is first to be strung, and then pulled a certain distance (or force) without breaking. This proved to be a more difficult simulation task than I initially thought it would be.
I have here produced a parametric design of a bow. The challenge is to deform it to a point where the string (=string force) is vertical. The next step is to pull the bow to, in my case a certain force. As the model is created now (force controlled), I can't specify a string length as input and then pull the bow with a given force (or pull distance). Instead, I have calculated the string length as a result. The problem with this is that in the initial analysis, the string length at time=1 (vertical string) does not necessarily become the same, as at time=2, when the bow is pulled to a 45 degree angle (vertical and horizontal components of string force are equal) . So I first have to set a string force, run my analysis, measure the string length at time=1. Then I need to make a second run, a sensitivity study where I vary the pull force, to find the pull force at time=2, that will give the same string length as in run 1, at time 1, with the original string force.
Example: As the model is now, I have deformed it to a string length of 446 mm at string force 150 N (bow stringed, not pulled). The next step is to run a sensitivity study where I vary the parameter controlling the string force, so as to get the same 446 mm string length at time=2, when the bow is pulled to a string angle of 45 degrees (this is assumed to be an input design constraint). It turns out that the pull force is then 259 N. The string force (at 45 degree string angle) is thus sqrt(259^2+259^2)=366 N when the bow is pulled.
The way I have set up the problem, I have strung the bow by applying the force with time functions that may seem strange; this is to ensure that the bow does not flip over to the other side, and the solver finds the wrong equilibrium position; bent forward.
Now to optimize the bow, I would typically want to maximize the change in strain energy stored in the bow, between time=2 (bow pulled) and time=1 (bow stringed, not pulled). At the same time, we need to keep the maximum stress below a limit. Ideally, the pull force, pull length, and maybe the bow length are design constraints,
I challenge you guys to come up with a more clever way to set up this problem, and run an optimization design study to maximize the change in strain energy between time=1 and time=2, with appropriate design constraints (stress, force, pull length etc). I have played with the idea to use prescribed displacements, but the way I approached the problem, I seem to end up in a situation where I need to activate/deactivate constraints at given times, and this is not implemented in Creo Simulate.
I also challenge PTC's developers to set up this problem from scratch, they might find some functionality they would like to add... (Or, maybe it's just me being stupid not being able to figure out how to set up the problem..? If so, enlighten me...)
Happy holidays, enjoy your bow modeling and may the force be with you!
/Mats L
PS. I should mention that I am a complete novice in archery, bow design etc. I think this is obvious when you look at my bow...
This thread is inactive and closed by the PTC Community Management Team. If you would like to provide a reply and re-open this thread, please notify the moderator and reference the thread. You may also use "Start a topic" button to ask a new question. Please be sure to include what version of the PTC product you are using so another community member knowledgeable about your version may be able to assist.
- Labels:
-
General
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
An interesting challenge! While I won't be having a go, I will be watching with interest.
In terms of maximising strain energy, assuming compound bows (with the string passing over eccentrics or cams) are not allowed(!), I believe the recurve form allows the string to roll off the limbs during draw, with the effect of increasing effective limb length during the draw and flattening off the force / draw length curve (or at least keeping it linear, rather than increasing in stiffness). Aiming towards a constant draw force should tend to maximise the stored energy.
Modelling a recurve design effectively is basically going to require modelling the string and using contacts between it and the limbs, I suspect...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And here's a relevant paper!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Someone out there is awesome:
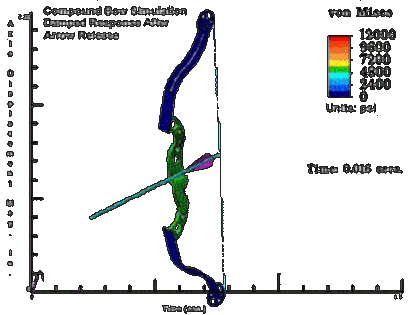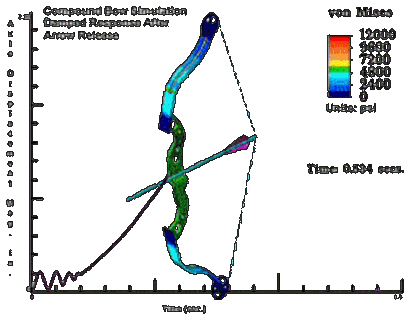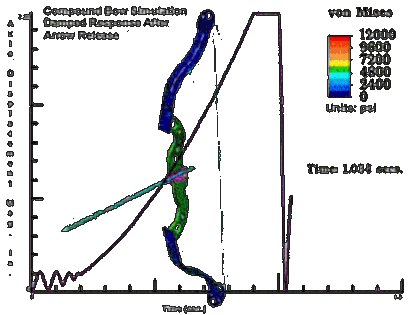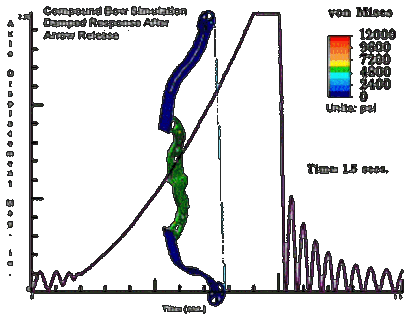
harvesting the fruits of the web | Compound Bow Simulation Damped Response After...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's very pretty, but he seems to have missed the actual function of a compound bow - the string doesn't appear to pass over the pulleys, and the draw force curve looks nothing like that of a compound - it should peak and then reduce towards full draw.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, my understaning of the compound bow is that your string turns cams located at the tips of the limbs, and those cams in turn, tighten additional strings, so as to get a "lever" for your draw force. By doing this you can increase the stiffness of the limbs considerably, and you can pull with a lower force and still store more energy en the bow.
These are nice presentations and all, but it doesn't help me set up the problem as i would like to, in Creo Simulate. I too can find the deformation and corresponding forces at stringed state, and drawn state, but only through "trial and error"... Ideally I want to enter max draw force, draw length, string length as inputs, and then have Creo optimize the bow for me. To begin with, let's ignore the contact between string and bow for the recurve design.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you will have to use the Optimization/Feasibility menu:
You will have to settle on more geometric items for the Design Variables such as thickness, height, etc.
Add them to the Design Variables list with a range of Min & Max.
Then complete a Mechanica Analysis.
You will have to decide what is your Design Goal because you can only pick one I believe:
Von Mises Stress of the bow.
I have used this before and it is very effective. Except Mechanica cannot auto converge the elements like Ansys can so you will then have to run your results 3 times with smaller and smaller mesh until the results are consistent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems the picture was wrong, the string preload at time 1 is 150*1.7=255 N... Otherwise correct...If you enter 150 N the bow will flip over and find the other equilibrium position.The factor of 1.7 is entered in the load time function table.





