Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
2 questions on Fourier transforms in Mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2 questions on Fourier transforms in Mathcad 15
1. Unless I am missing something, there is a inconsistency in the time conventions of the fft and the symbolic Fourier transform function, fourier. See attached
2. Has anyone developed a Filon technique Fourier transform in Mathcad 15?
Thanks,
Reg
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Reg Curry,
there is a whole collection of mathcad inconsistencies, to which we can add this on the Fourier transform. It follows a comparison with the Wolfram results:
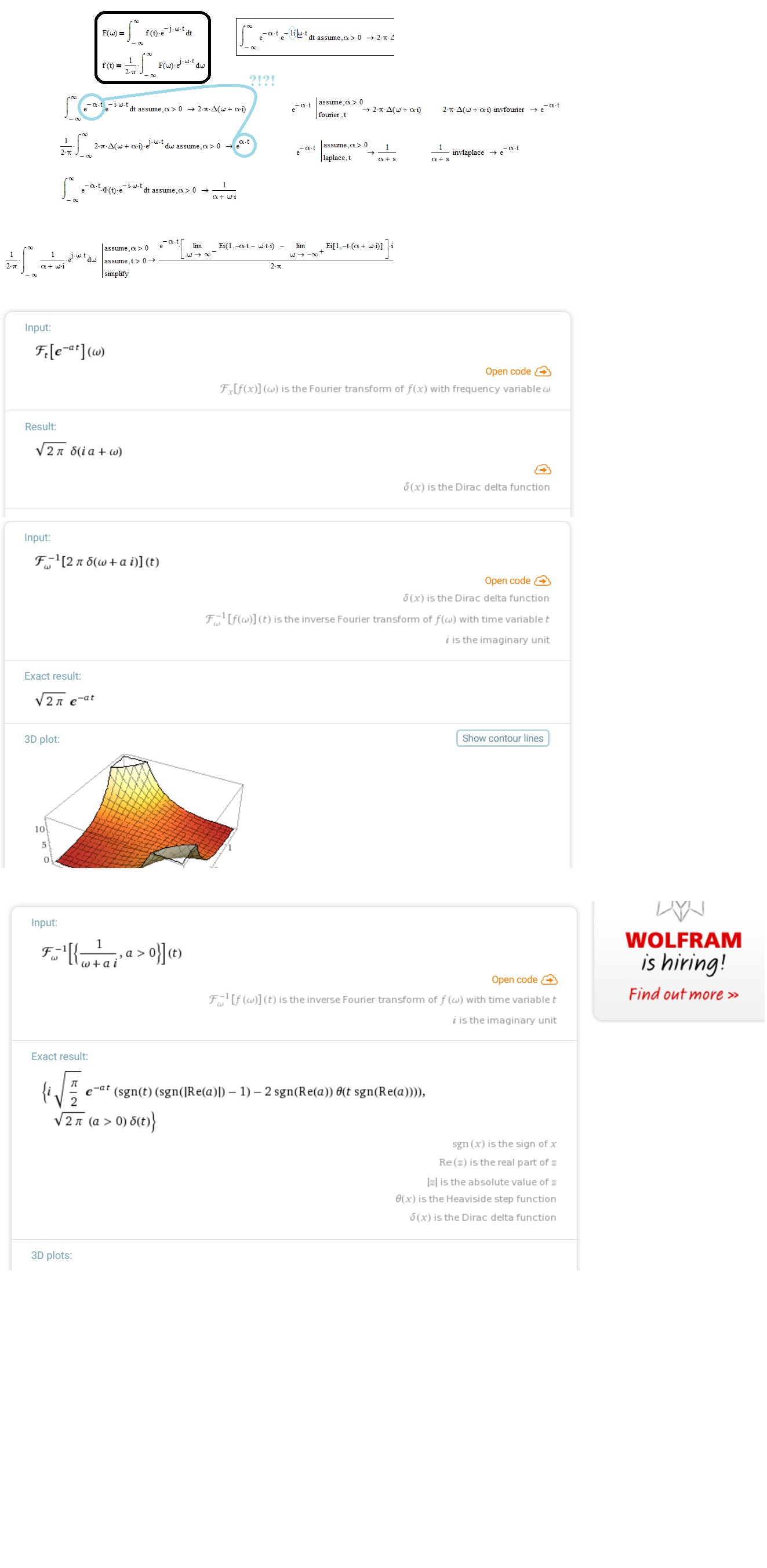
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Reg Curry,
there is a whole collection of mathcad inconsistencies, to which we can add this on the Fourier transform. It follows a comparison with the Wolfram results:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M.--
Thanks much.
By the way, how did you input the programming version of fourier built-in function with alpha >0 ?? When I try to add a programming line the symbolic arrow appears only after the alpha >0, and not for the whole expression. There is clearly a syntax input I don't understand for using constraints with the built-in functions in programming mode.
Thanks again.
Reg
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In summary, with F.M. help above, attached is my summary of inconsistencies between symbolic integral Fourier Transforms and the built-in Symbolic Fourier Transforms.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

2) Could you be interested in the stationary phase method?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M.--
Thanks much again. You have really helped.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good day Reg -
Welcome again to PTC Community - so glad you could find a solution.
In order to help others who are reading this discussion, and make the knowledge easier to find, would you please mark the most helpful answer as correct?
Best,
Toby
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I used to do complex electromagnetic calculations in the frequency domain and then transform the results to the time domain using Filon's method. This was all done in Fortran. Since retiring several years ago I no longer have those Filon Fourier Transform codes on which to build a Mathcad Filon worksheet and my memory is not what is once was. :>(
The nice things about Filon's method is that you don't have to have uniform steps in frequency or time. You can define a specific number of points per decade and then define the number of decades over which to perform the integrals, thus greatly reducing the number of points for the transform. The transforms back to time give both an even function and an odd function in time. If both of these results are identical, then you know the transform is good. If not, then the number of points per decade can be increased as well as the number of decades included in the transform.
Thanks again for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can you be interested in the following?
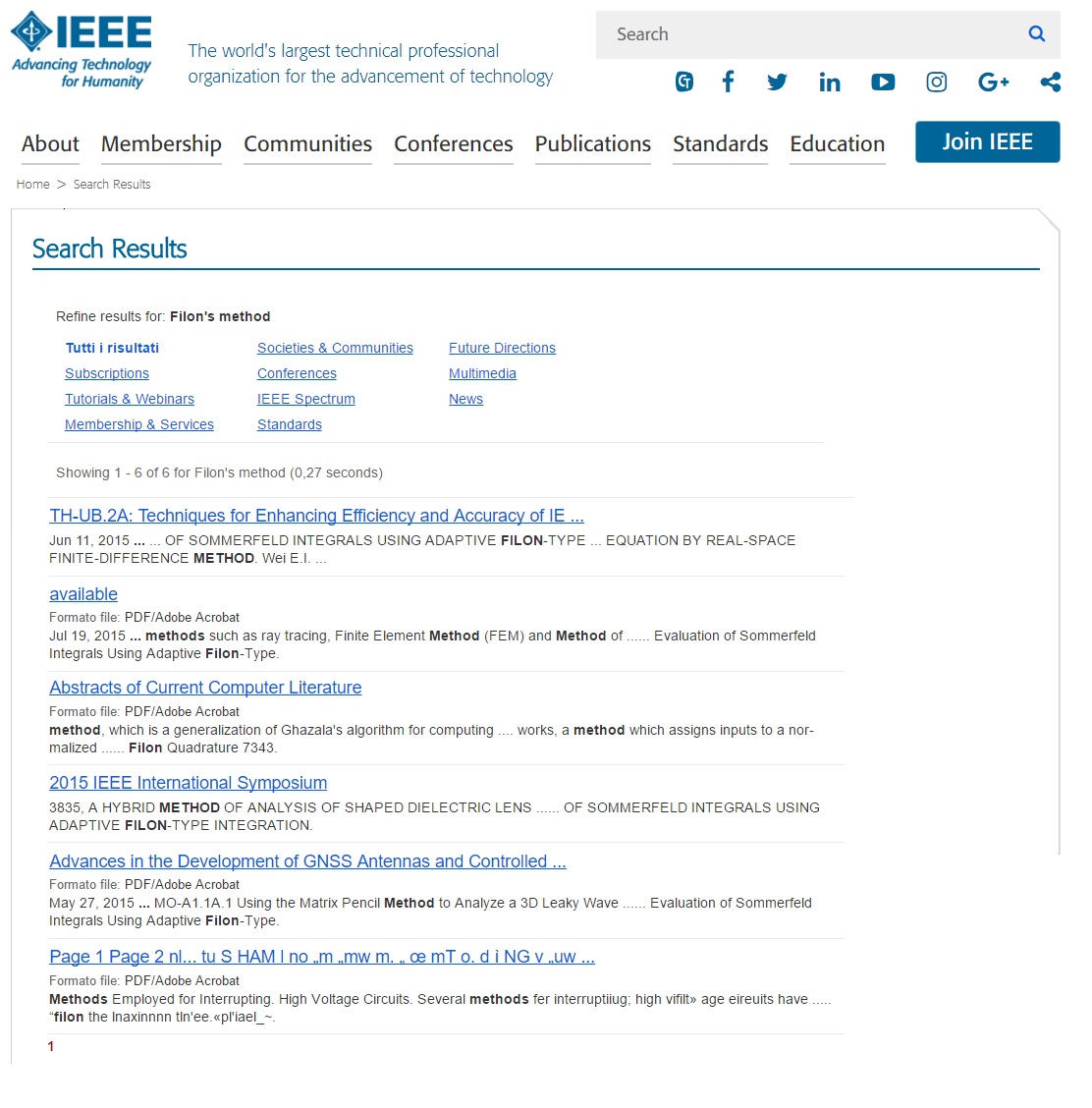
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M.,
Thanks. I am a life member (due to age) of the IEEE. I will see what is available in those references.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi R. C.,
I am a member since a few decades. But I read articles published on some magazines (IEEE proceedings, and others) from the seventies of the last century.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad (I guess 14 and up as well as Prime) is fooling you. Blame MuPad..
You hadn't tried the integral in Wolfram Alpha, then you would have seen that the first integral does not converge:
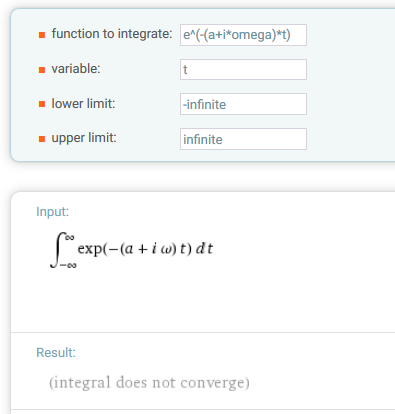
I get the same in Mathcad 11:
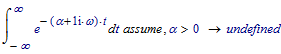
Looking up my old textbook I find (and remember) that there is an important property required for the function undergoing the Fourier transform:

in this case. It must be absolutely integrateable over all t, that is:
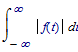
must converge. For the f(t) given that's not the case, even with alpha > 0.
But with a small adaptation all is OK:
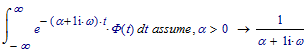
Of course using the fourier transform symbolic function and its inverse gives a nice pair:

Luc





