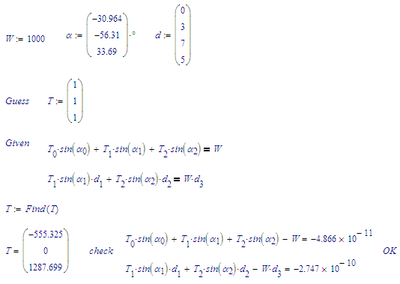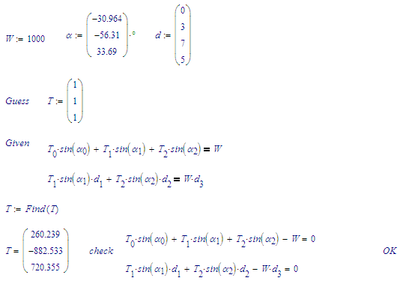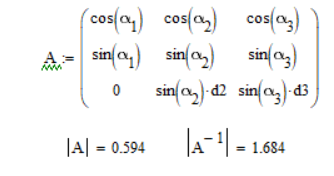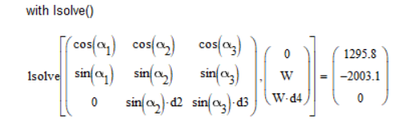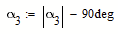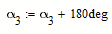Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
3 unknowns, 2 equations solved in mcad15 !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
3 unknowns, 2 equations solved in mcad15 !
To all
Q : How is it that mathcad 15 can solve a 3 unknowns , 2 equations problems?
Background
I suspect I am overlooking something so obvious as to be embarrassing. I was writing down some “blocks” of stuff to figure out/decide how to set-up some syntax in mcad for a larger worksheet. Doing so I copied-and-pasted some equations from another worksheet and to my surprise mcad solve the problem i.e. I got number out! See attached
This is based on static equilibrium Sum of force = 0 & sum of moments =0
I added a 3rd equations (sum Fx=0) and mcad solve it too – fair enough
I simply can’t quite get it – The issue is both math fundamental and understanding Mathcad. Hopefully some of the expert (you know who you are guys) can enlighten me on this
Thanks in advance
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad will give you the first solution its algorithm is able to find. In case of 3 variables and only 2 equations mathcad has the freedom to chose any of the (usually) infinite number of solutions. Which one it choses depends on the way the underlying algorithm is working and may also depend on the guesses and on the equations themselves.
Right click the word "find" and you will see that the algorithm is set to linear (which is perfectly OK given that equations actually are linear). Using "linear" algorithm usually sets the "superfluous" variables to zero and solves the system. Why in your case T2 is set to 0 and not the last one (T3) is beyond my knowledge. We would have to know how exactly the algorithm is implemented to find out which logic it is following.
Right clicking "find" you may also change the algorithm to "Nonlinear" and play around with the three algorithms offered and their options. You may get a couple of different solutions but each one actually solves the two equations and therefore is correct. I thought that Mathcad would freeze one of the variables to its guess value and solve for the other two, but in case of your underdetermined system it doesn't. Again we probably can't say why without knowing the exact implementation of the algorithms.
For a further set of solution you may also use the "lsolve" function. I would have expected that a solve block with the equations given in matrix form return the same results (with algorithm linear) as lsolve, but, alas, it doesn't:
Here are two simple examples of one equation in two variables and the solutions given with the various algorithms. As you can see using Levenberg-Marquardt apparently the nature of the equation determines which variable is frozen.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. I guess it's the "same" idea/problem. Not sure I understand the solution to the link posted - Beyond my math level I guess. One does not understand why mcad 15 solve the problem. If one was to put numbers for a real problem to solve then one gets answer. One of those "computer gave me numbers so it must be right" moment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have not one but a set of solutions!
New guess values - new solution!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
not when I try with new guesses !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You didn't try hard enough. Your solution is one of many:
If you change the solve method (right-mouse on Find), to Levenberg-Marquardt, you get:
But with Conjugate Gradient, or Quasi-Newton, no solution is found.
And of course, the symbolic solver doesn't find a sulotion:
But with the third equation:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You haven't finished the problem; There are vertical and horizontal components of T1, T2, and T3.
Sum of horizontal forces must equal zero as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad will give you the first solution its algorithm is able to find. In case of 3 variables and only 2 equations mathcad has the freedom to chose any of the (usually) infinite number of solutions. Which one it choses depends on the way the underlying algorithm is working and may also depend on the guesses and on the equations themselves.
Right click the word "find" and you will see that the algorithm is set to linear (which is perfectly OK given that equations actually are linear). Using "linear" algorithm usually sets the "superfluous" variables to zero and solves the system. Why in your case T2 is set to 0 and not the last one (T3) is beyond my knowledge. We would have to know how exactly the algorithm is implemented to find out which logic it is following.
Right clicking "find" you may also change the algorithm to "Nonlinear" and play around with the three algorithms offered and their options. You may get a couple of different solutions but each one actually solves the two equations and therefore is correct. I thought that Mathcad would freeze one of the variables to its guess value and solve for the other two, but in case of your underdetermined system it doesn't. Again we probably can't say why without knowing the exact implementation of the algorithms.
For a further set of solution you may also use the "lsolve" function. I would have expected that a solve block with the equations given in matrix form return the same results (with algorithm linear) as lsolve, but, alas, it doesn't:
Here are two simple examples of one equation in two variables and the solutions given with the various algorithms. As you can see using Levenberg-Marquardt apparently the nature of the equation determines which variable is frozen.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks to everyone for the reply. I knew some of you guys couldn't stay away 😊. Very glad and I am glad I asked the question. The whole things goes against what one is taught about solving equations. N variable needs N equations. Given that mcad spits an answer if one was in a rush and/or the problem a bit more complicated then could believe the answer
I noticed about the linear/non-linear option but at this moment in time I am not changing this because I don't know the differences (when to use, etc) and would need to read about them 1st. The set of equations are always linear- standard mechanics stuff - sum of forces, etc
So before I "close" this questions: Even with 3 equations, there are an "infinite" number of solutions?
I just tried the lsolve() as suggested & demonstrated by Werner_E with 3 sets of equations and indeed the answers are different Correction: Get the same answer. Maybe need to ditch equation #1 (Sum Fx =0) and introduced a displacement-relation (indeterminate static problem)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Even with 3 equations, there are an "infinite" number of solutions?
That depends on the equations.
If they are not linear independent then there might be an infinite number of solutions.
Given three equations in three variables also might not have a single solution as well.
Three linear equations in three variables only have one single unique solution if the determinant A of the matrix of coefficients is different from zero. That way the matrix is invertible and you can solve the set of equations A*x=b by x=A^-1*b.
If det(A)=0 the system may have no solution or an indefinite number of solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Forgot about this !
Using the lsolve() set det(A) is not zero if I got this right
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"So before I "close" this questions: Even with 3 equations, there are an "infinite" number of solutions?"
No, Because you missed an equation (for horizontal forces.
There's one answer, and if it looks strange then you and I have screwed up the constraints.
Attached is Prime 4.0 Express and a pdf of that file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred
Thanks a lot. I am getting this too
T3 = 0 seems odd
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just a thought - are you sure about
Could it be rather
After all there is a symmetry btw T2 and T3 wrt W.
In this case det(A)=0
Another remark: Instead of angle(...,...)-360deg you could also use atan2(...,...)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I need to check this as you might be right. Might be a “left over “ of something I was playing with and left it behind. Well spotted
Thanks for the atan2 hint as well
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That no unique solution to the three support problem exists can be demonstrated.
Attached is a vector treatment of this problem, which simplifies the understanding of the relationships. Any two of the three supports will result in a unique solution; some of them better than others.
Just putting "PAID" to this issue for myself.