Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A water flow problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A water flow problem
Okay, here's the challenge: measure the flow rate of a stream.
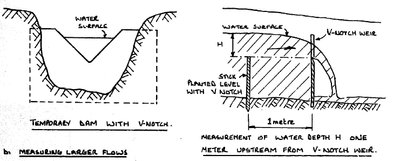
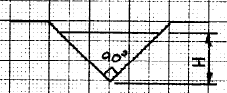
- Build a weir with a V-notch as shown below,
- measure the water depth as shown.
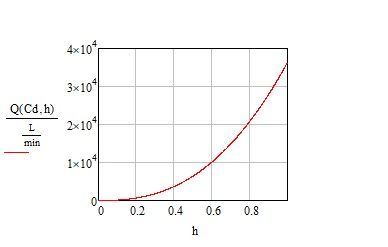
What is the flow rate (liters/min) for a given height H? A derivation and formula, please!
Solved! Go to Solution.
- Labels:
-
Civil_Engineering
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know very good handbook on this field of science. But in Russin.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have a look at Ken Edward's stuff at LMNOeng.com He seems to have solved this problem quite well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is an interesting illustration of engineering adapting physics.
Both Alan's solution (kudos, BTW) and the one attached below properly derive the physics of the problem from basic concepts: the gravity head creates a flow over the weir, and that times the area gives the flow rate. But when the actual flow rate was measured it fell significantly short of what was calculated.
The old engineers, well used to having theory only approximate reality (because of the assumptions made to achieve a solution) merely created a "coefficient," to adjust theory to reality. It would be interesting to see what ANSYS would do with this problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"The old engineers, well used to having theory only approximate reality (because of the assumptions made to achieve a solution) merely created a "coefficient," to adjust theory to reality. "
Engineers regularly do this, of course. They have discharge coefficients, friction factors, loss coefficients etc. The nuclear reactor physicists I knew would never stoop to such common or garden terms. When their theoretical rod positions didn’t quite match the measured ones, they modified their theory by an eigenvalue bias (a rose by any other name…!)
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's been my observation that there are two types of "coefficients":
- Coefficients that account for "general cases" where the physics is understood but the problem is too complex for a direct solution. Airfoil lift and drag coefficients are an example. There are tabulations of these coefficients for a given airfoil (defined by a set of coordinates, ratioed to chord length.) That coefficient, multiplied by the dynamic pressure and a scale measurement, will give the force that you will measure with the proper equipment. Size (within reason) doesn't matter, which is why wind tunnels are such useful tools--by testing smaller (and therefore cheaper) scale models, the coefficients can be calculated and the performance of the "full scale" article can be computed. (Only recently have computer models begun to approximate the accuracy of wind tunnel testing; and cautious managers still require a careful comparison between model predictions and wind tunnel measurements.)
- Coefficients (like the "discharge coefficient" in this discussion) that are required to account for something the physical theory does not explain. This is a dangerous area, where application of an equation with a coefficient may yield a result that is grossly inaccurate because the equation is based on a physical theory that no longer applies. (I spent a career "opening the lids of closed black boxes" to understand what the assumptions behind the equations were.) It was gratifying to see Alan develop the theory, then (citing a reference) select an empirical coefficient to adjust for an unexplained deviation from the theory.