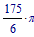Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Bicycle pump
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bicycle pump
I need not simple solution, but best solution! Слабо?
- Labels:
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My own solution in my own Mathcad with correct temperare base unit (not kelvin but J/mol) and correct ideal gas law (not p v = R T, but p v = T)
Wath can you say about my own Mathcad?
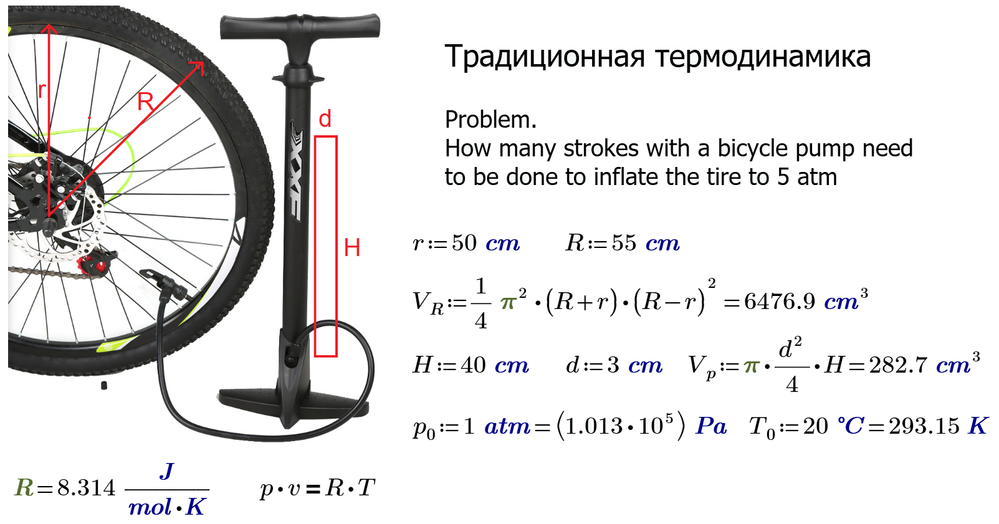
Assumptions. 1. The bicycle tube does not change its volume when inflated (the tire is quite rigid). 2. The air temperature in the chamber and pump does not change.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
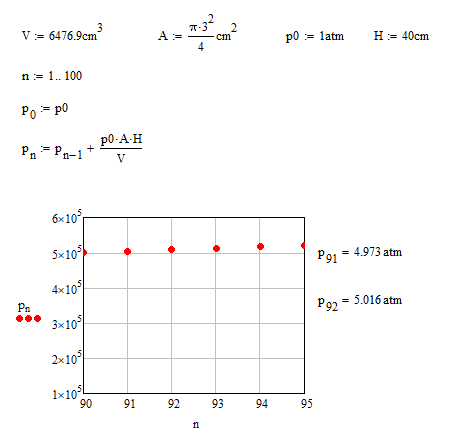
Verify
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't know what qualifies as the "best" solution, but here's a totally different approach. I note that, if the temperature is assumed to be constant, the pumping must be done very slowly indeed, as my experience with pumping tyres is that the pump rapidly gets hot!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The answer is exactly:
which is about 91.63
Derivation:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice funny story about slowly.
One filmmaker was very fond of actresses and "closely communicated" with them a lot.
This filmmaker had a heart attack and was hospitalized.
After the treatment, he set to work on the old with actresses.
One actress asked him: "Can you do THIS?"
The filmmaker replied: "I can! But slowly!"
Harassment or not harassment? It is a quastion!
If slowly - not harassment!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's my attempt. I'd challenge the assumption of a toroid, but that's a detail. The discussions about temperature are moot, imho. You want a pressure defined while you are riding, when any pumping temperature rise has long since dissipated. Pump it up and then check it later. Also the thermal mass of the pump and tire >> thermal mass of air. (and pressure recommendations already take into account any running tire heating, at least for cars) To me the problem is a mass transfer problem.
Answer: 31.6 strokes which seems reasonable since I've pumped up many bicycle tires.
Edit: Had some Z typos.
Edit 2: I just saw the target pressure was 5 atm. So that answer is 91.796 strokes. Which seems high, until I noticed the tire is gigantic at 110 cm diameter.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
92! 31! Who will offer fewer pump strokes?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My attempt to calculate trmperature by adiаbatic process (no loss heat)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is my take
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
109! 92! 31!
Who will offer fewer pump strokes?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
On more solution (Prime 6 in attach). Assumption - the air temperature in the bicycle wheel chamber has risen by 10 degrees Celsius (10 kelvin)
This answer is the most beautiful - 88 (butterfly)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator