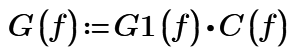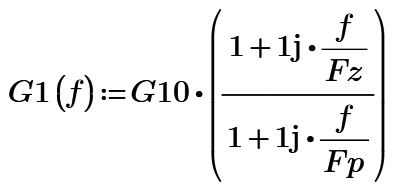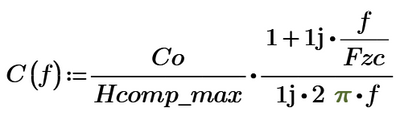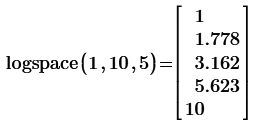Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Bode Diagram Plot
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bode Diagram Plot
Hi,
I am at my first steps with Mathcad, could someone help me to plot the bode diagram of the function G(f) pease
Where
and
Thanks
ML
- Labels:
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please first enter your formulae onto a Mathcad worksheet and attach that worksheet to your posting.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
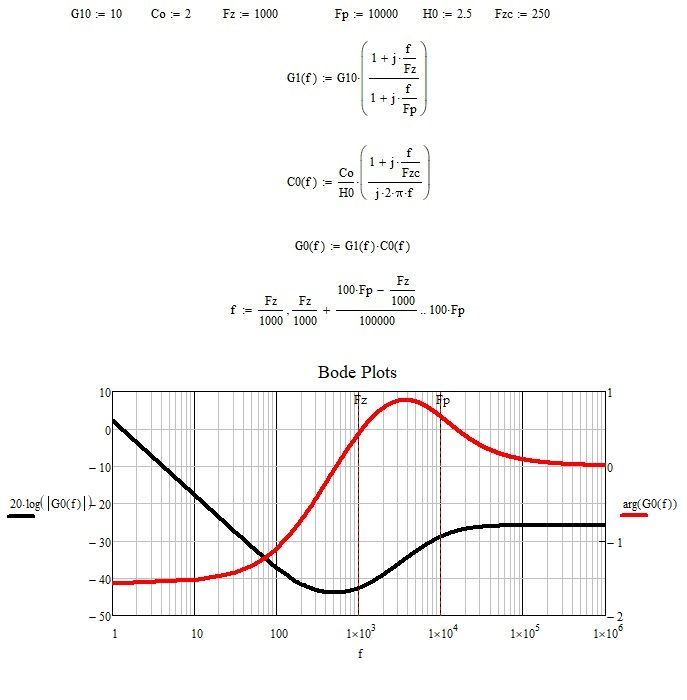
I randomly established the values of the constants.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your answer but could you please explain how did you get the definition of the frequency range ; and some steps to plot the diagram as you did.
thank you,
Regards.
ML
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can define the frequency range taking as minimum frequency the smallest value among the absolute values of the poles and zeros and as maximum value of the frequency range, the maximum value among the absolute values of the poles and zeros. The step amplitude can be defined dividing the difference of the previous values by the number of steps. I have considered as a minimum value of the frequency Fz divided by a thousand and as a maximum value, Fp multiplied by one hundred. To have a larger diagram you can replace a thousand with ten thousand and one hundred with a thousand or ten thousand or even more, that is, they are chosen according to your needs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
i get the explanation about the frequency range definition, thank you
Now trying to reproduce your same example in mathcad,i can't get the same diagram as yours. How do you do it?
I would like to learn doing it clearly as you do. Some tips please.
In the picture what i get when i plot the diagram with the same values.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please attach your Mathcad worksheet....!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just send the necessary informations to plot the bode diagram.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
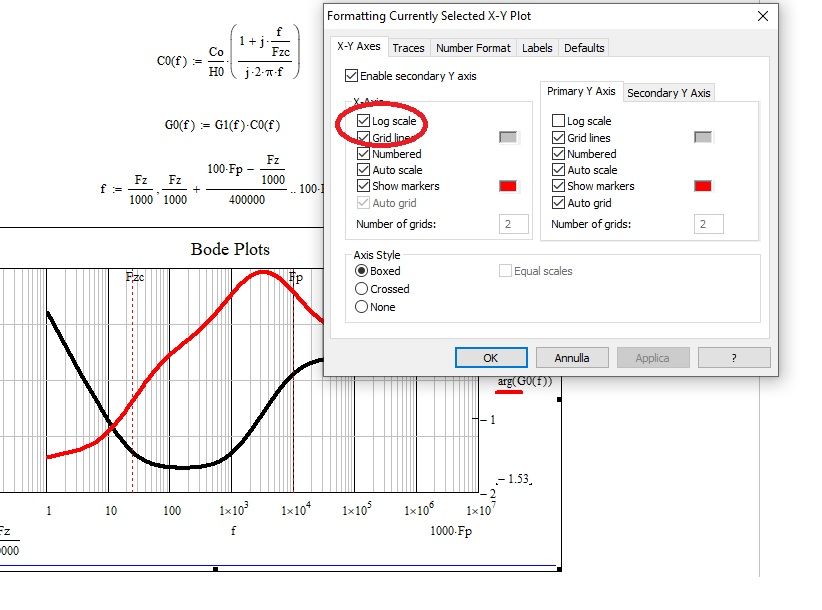
By quickly double clicking on the graph, the following panel appears with all the options. You have to choose log scale for the x axis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have MathCad 6 Prime installed on my pc, i can't access these functions to edit the diagram...it is about the program version?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
FIRST and before all: Attach your mathcad worksheet.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As an alternative, to generate the logarithmically spaced frequency points, you can use the logspace function. Supply it with first (smallest) and last (highest) frequencies, and the number points per decade, gives you an array of frequency points. Like this (for 1 to 10 with 5 steps per decade):
Success!
Luc