Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Cable length
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cable length
Hi
How would I solve the following problem on cable length
Thanks
Two cables, both with cross sectional area 5 mm2, are connected in parallel across a common DC voltage of E = 36 V.
The resistivity of Cable 1 is ρ = 17 x 10-9 Ω.m at 20 °C, while the resistivity of Cable 2 is ρ = 28 x 10-9 Ω.m at 20 °C.
Cable 1 is 1641 mm in length.
If 44.9 % of the current passes through Cable 1, determine the length of Cable 2.
Assume the ambient temperature is 20°C.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can use the current sharing ratio and Ohm's law to determine the relative resistance of the two cables. They're both the same area. Resistance is made up of resistivity cross-section area (the same) and length.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
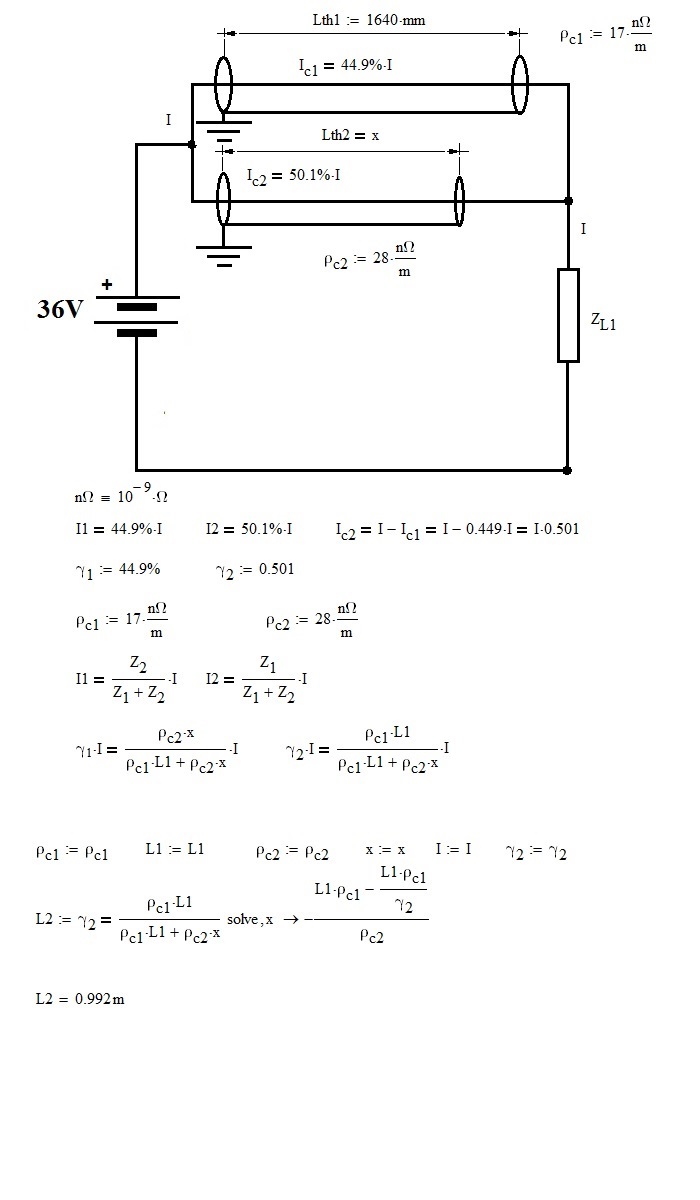
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tend need to disagree.
Note that 44.9% and 50.1% do NOT add up to 100%...You're violating Kirchoff's law.
Also note that the resistivity is (correctly) given in nΩ.m, not in nΩ/m.

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
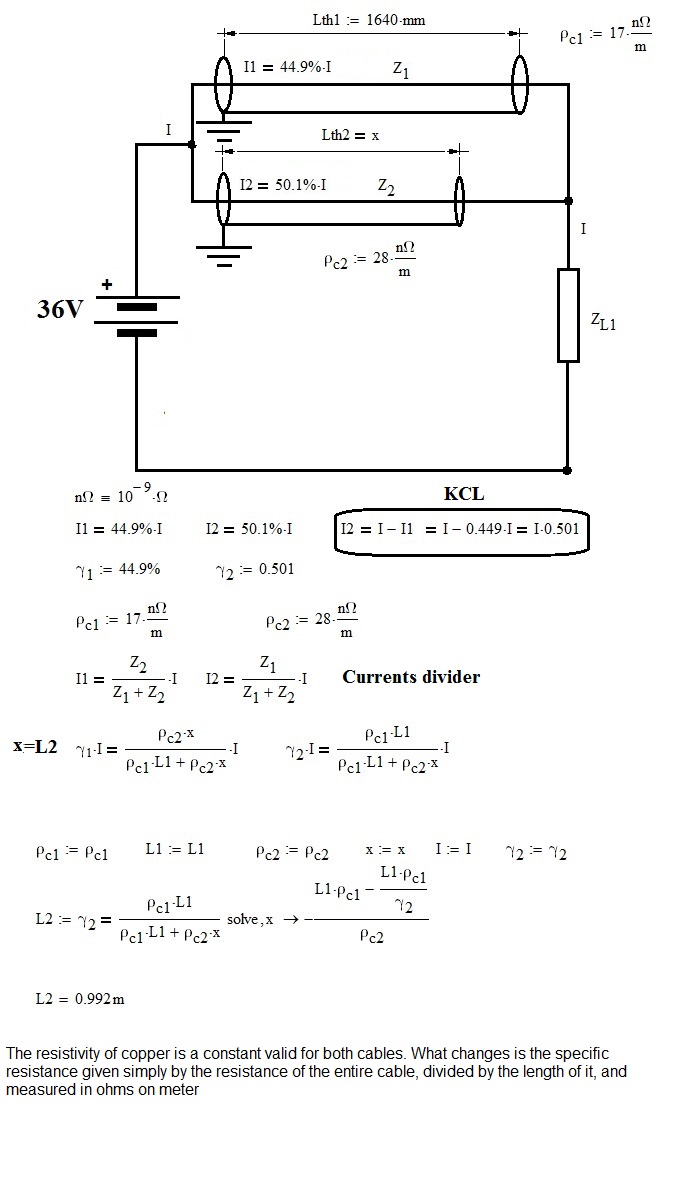
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Check your math!
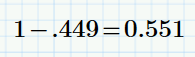
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The drawbacks of on-line haste ....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Commonly the cables are made of copper.
I made the calculations based on this hypothesis.
it is obvious that if a cable is copper and the other is silver, resistivity and specific resistances are different.
Bye
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I do not think the material name (i.e. copper) does matter in this case. The specific resistivity is given for each of the two cables, and they're different. If one is copper, the other isn't.
Your (now encircled) equation cannot be correct. If one cable carries 44.9% of the current, the other MUST carry the remainder, that is 1- 44.9 %= 55.1 %.
You draw a Z.L1 in your circuit. That is not given in the assignment; and it wouldn't matter if it were.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Considering my hypothesis, (both cables copper), the calculations are correct. (Sorry, in the calculations I wrote 0.499 and not 0.449).
I believed that the applicant was referring to the specific resistance of each cable (and that he had made a mess) and not to the resistivity of each.
In the latter case, you're right.
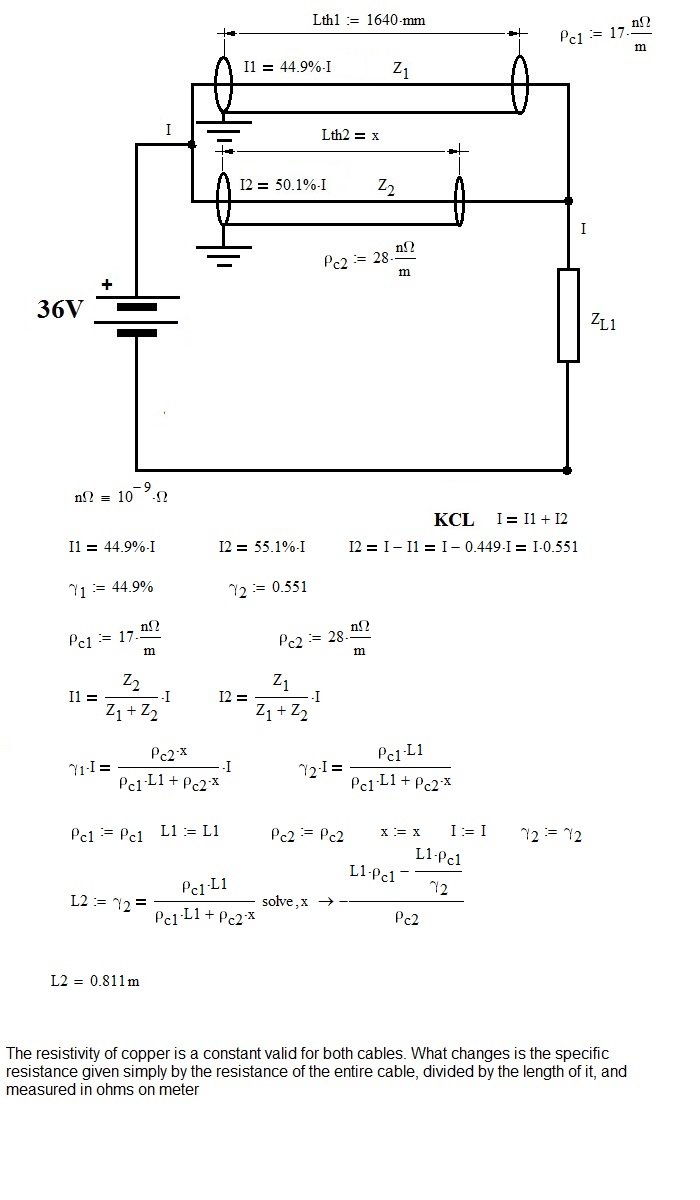
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK.
I still have a problem with your definitions of rho.c1 and rho.c2.
The (specific) resistivity is a material property, commonly denoted by the greek letter rho, and it has the dimension Ohm * m, or sometimes Ohm * mm^2 /m to indicate that the resistance of a wire increases with length (in m) and is inversely proportional to the crossectional area (in mm^2). So never Ohm/m !
I've found one place (of many) where such resistivities of materials are given: Table of Resistivity.
With rho.copper given as 1.68*10-8 Ohm*m, it could be that cable 1 is of copper. Then cable 2's rho closely matches that of aluminum (2.65 *10^-8 Ohm * m.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm a bit precipitous, which leads me into error. I'm sorry.
I rewrite the calculations, as had to be done. (the results are the same, though)
greetings Franc

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
I have tried to copy what you have done but end up with undefined variable.What am I doing worng
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good evening Aaron Garson!
Do not worry, I am attaching the file
Greetings f. M.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's because the variable (gamma2) you are trying to evaluate is actually not defined. It is only used in writing up equations involving a 'hard' equals sign "=", which means "is equal to". For definitions you must use an assignment symbol ":=", which you normally get by just typing the colon.
But besides that, you're not looking for that variable, gamma2 should be defined as 1-gamma1, where gamma1 in turn should be defined as 44.9%.
In the solve you're trying to get at x, and that variable should be available once you have defined gamma1 and gamma2 and L1 properly (define them just like you did nOhm, rho1 and rho2.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Relevance of the copper - silver argument? Just use the data given - no need to infer the material.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
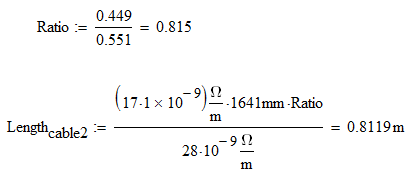
The 0.449 and 0.551 is the current split ratio.
All other numbers are self evident from your initial question.
You can spruce it up with a better labels and definitions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are also a some cheat which can be do with this set of equations.
Actually, the "hide" is only for show the equations, but it not necessary.
Best regards.
Alvaro.
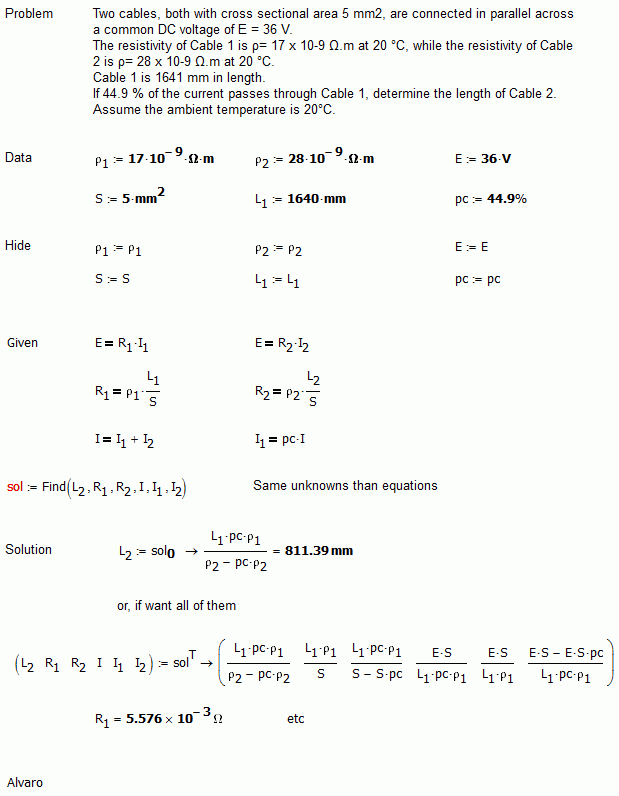
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cable length is 1641mm not 1640mm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I loose a milimeter attaching the wire to the battery 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is also a physical impossibility problem with the way this question is drafted. The cables are NOT "connected in parallel across a common DC voltage of E = 36 V." They would have to be connected across a much lesser voltage. While not mentioned in the question the sketch shown in the replies show a Zl1 where most of the voltage would be dropped (which would be a real world connection). If the cables were connected across 36V they would have to carry approximately 2.87 million Amperes. Good luck with that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi. That's what mean a shortciruit. But still have some applications. For example, as lamp, with power about 250 kW for each wire, or to use the wires to cut something by heating them.
Also, a good time to remember that Ohm law isn't a true "law", it is a rule, which sometimes hold, but not always. If the wire explode, them Ohm law don't apply.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A little remark from Mathcad Server - not ohm*m but ohm*m^2/m:

And second - do not use two different metals in one circle ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems that .... with these two cables .... we put "meat to cook" ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator





