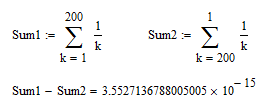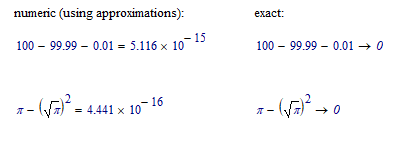Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Can anyone explain this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can anyone explain this?
Hallo,
found something strange in the calculation when i show all decimalpositions

Is there any plausible explanation?
lg
Stefan
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
digital math accuracy.
Early on in my class on FORTRAN we covered the fact that each computer math operation introduced the possibility of a small random error, and that these accumulated If you add (or multiply or divide) a sufficiently large quantity of numbers you will get an incorrect answer. This introduced the concept of significant digits; and that's what you're illustrating--the last digit in your response (and based on the two decimal length of your inputs quite a few of the trailing zeros) are not significant.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You will see similar effect with most software which uses the usual IEEE fomat to store floating point numbers.
This format will provide a precision of 15-16 decimal at max.
In case of Mathcad there is additionally a chance that numerical roundoffs are introduced by the use of units. The units you provide are converted to the base units, then the calculation is done in base units and for display the result is again converted to the units you demand to see.
The error you show is just 2*10^-18 m.
If you really need more precision you'll have to use the symbolics.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you,
is not relevant but iw a sjust wondering myself.
lg
Stefan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
An old favourite calculation on computers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's another classic one:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
digital math accuracy.
Early on in my class on FORTRAN we covered the fact that each computer math operation introduced the possibility of a small random error, and that these accumulated If you add (or multiply or divide) a sufficiently large quantity of numbers you will get an incorrect answer. This introduced the concept of significant digits; and that's what you're illustrating--the last digit in your response (and based on the two decimal length of your inputs quite a few of the trailing zeros) are not significant.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did you know that 100 – 99.99 – 0.01 = 5.117…x10^-15? Well, according to most software, it is. 🙂
In all my years of testing this and similar subtraction problems, the only things that always produced the correct answer were my Hewlett-Packard and SwissMicros calculators (which use binary coded decimal rather than floating point math), Q&A 4.0 (an old DOS-based database program) and Word for Windows 2.0. Q&A 4.0 and Word for Windows 2.0 accomplished this by rounding off the result to something like 7 or 8 decimal places. Newer versions of Word, and various versions of Autocad, Supercalc, Excel, Mathcad, etc. all produced the non-zero answer above due to the limitations of floating point math.
Thomas Okken's Free42 simulator of the HP-42S calculator comes in two versions: binary (IEEE floating point) and decimal (BCD). The binary version produces 5.117…x10^-15 and the decimal version produces 0. My SwissMicros DM42 calculates with 34 digits (!), but it uses BCD and produces 0. The DM42 also has an incredible dynamic range of about ±10^±6145.
BTW, some subtraction problems similar to the one above do produce zero using floating point math, it just depends on the specific numbers being used and the precision to which the calculation is being carried out. I have a spreadsheet at home with several hundred successful and unsuccessful calculations of the same form and which software I tested them in.
Why do I test this type of subtraction problem when tiny, non-zero results are irrelevant to the types of civil engineering problems I encounter? Because I sometimes have to test for zero, a non-zero result for zero causes all sorts of problems, and I need to know how each software program responds. So, the moral of this story is to round off or set a tolerance before testing for zero.
However, I believe the larger moral of this story is that the IEEE floating point standard is flawed. Back in 7th grade math in the early 1970s, I learned the following "tests for reasonableness":
(a) When adding or subtracting, the result can have no more decimal places than the operand with the greatest number of decimal places.
(b) When multiplying, the result can have no more decimal places than the sum of the number of decimal places in the two operands.
So, why aren't these tests implemented in the IEEE floating point standard, or if they are why aren't they used by programmers?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're speaking directly to my statement about significant digits. (Kudos for providing actual guidance!!)
Why isn't i handled at the program level? I can think of several scenarios:
- The programmers expect you to handle it, (In some cases they have, reference TOL and CTOL,)
- The programmers don't care.
Since Mathcad (before Prime) had an adjustable setting for zero it was possible to stop this type of debate on display (If the answer is less than xxx, display a zero.) Prime doesn't have that--refer to scenario #2.
Clearly you have encountered this problem and have certainly developed methods of dealing with it; most of the experienced users have. With all that's missing from Prime I would encourage PTC to divert programming power from this issue to address something more pressing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Im going to hope that ill never run into a mechanical engineering calculation problem were that tiny failures mather
because then im screwed up and never use Mathcad 15 anymoore lol.
Thank you for the explanations....
For example:
Actual real wallthickness: 16mm
Calculated required (without that failures): 16,00001
Calculated wallthickness (with that failure): 15,99999 (checking in Excel if OK/NOK)7
Smath doesnt produce this strange result in the calculation.....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Neither does Mathcad, if you use it correctly:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thats really wired...
is there a workaround for a correct calculation?
as my first ppicture?
In mathcad i can set the decimalposition to replace the result with a zero i just saw it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's even better than the BCD numeric approximations with rounding that e.g. the HP 42 calculator gives.
Success!
Luc.