Plotting Points ?

[lvl107]

   Hello, Everyone.

   From :

  How to plot 8 upper-corner-points ?
     Thanks in advance.
         Regards.

[ValeryOchkov]

[LucMeekes · Accepted solution]

Like this:

Success!

Luc

[lvl107]

   Your method to solve it, this is a new to me !  Many thanks for your time and help, Luc. I got it. 

        Best Regards.

[lvl107]

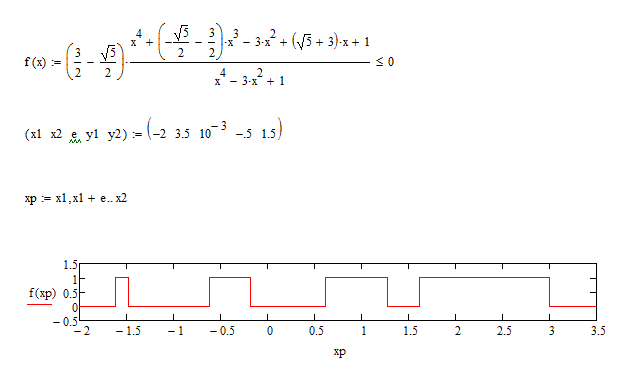
Luc, I don't know the reason the plot doesn't show up in this case.

    Regards.
         Loi.

[Werner_E]

You have disabled the plot region!

Right click the plot region and chose "Enable Evaluation"

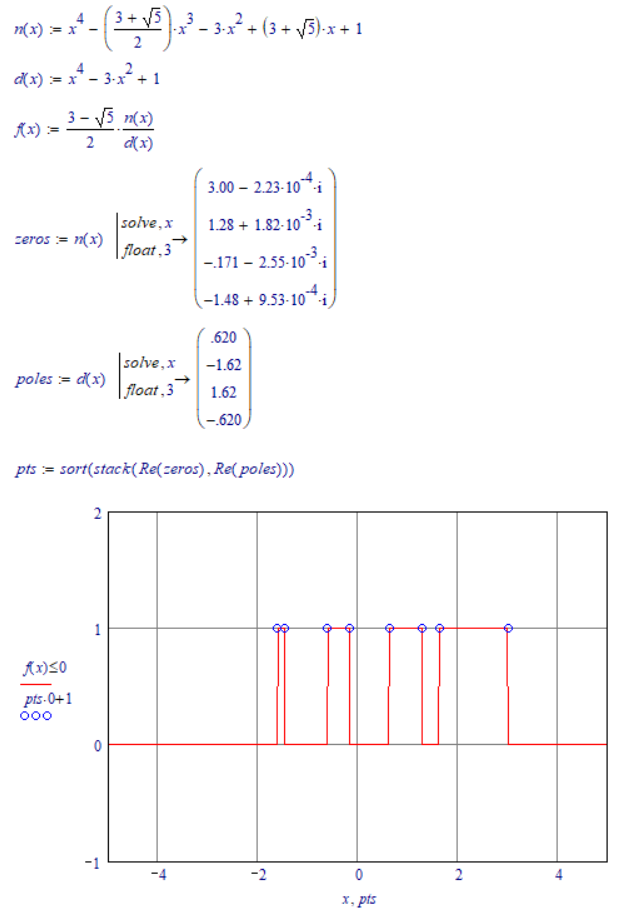
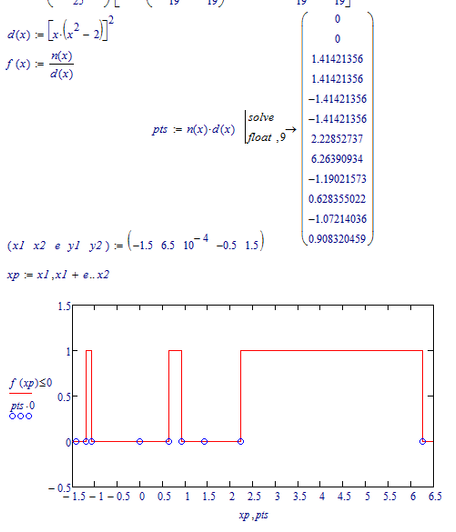
As you can see the poles at +/-sqrt 2 and 0 are no valid solutions to your problem this time. This is because they are poles of second order (the square in d(x)) and so there is no change of signs at those positions. A sign change only occurs at poles of odd order.

[lvl107]

   Many thanks, Werner. And how to keep the same "procedure" and eliminate 3 points are not 6 lower-intersection-points ? ( maybe just edit ? ). ( And how to plot local minimum-points of the f(x) ? )

   Best Regards.

[lvl107]

Correction : plot local minimum-points of the f.0(x) 

[Werner_E]

---

@lvl107 wrote:

   Many thanks, Werner. And how to keep the same "procedure" and eliminate 3 points are not 6 lower-intersection-points ? ( maybe just edit ? ).

---

You may think beforehand and don't ask for the zeros of the denominator which are of even order. In your example obviously all are of even order and so you would not ask for d(x)=0 at all.

As an alternative you may consider writing a function which eliminates all points of zeros (nominator and denominator separately) which occur an even number of times. This routine also must consider removable discontinuities like when nominator and denominator have a common zero. Good luck!

[lvl107]

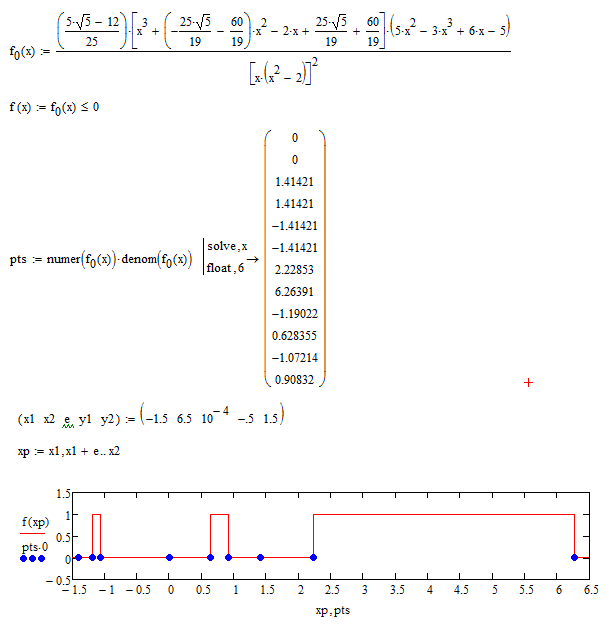
Luc, after I have got all of your hints, I try to plot all lower-intersection-points of logical-plot, but I don't know it's true for all of cases :

       Best Regards.

           Loi.

[lvl107]

  Oh, my trial is fail.

      Missing point.

[-MFra-]

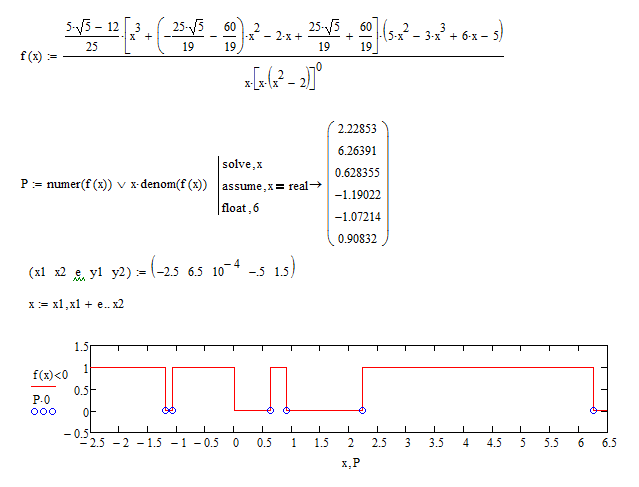
Hi,

You could also use the "numer" and  "denom" functions as shown:

[Werner_E]

or more compact:

[lvl107]

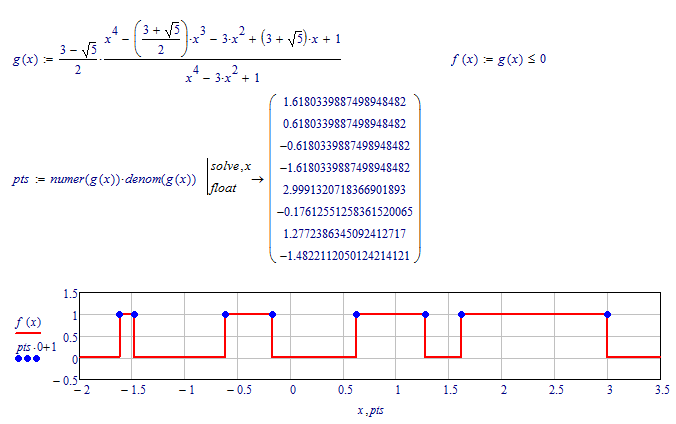
  F.M. and Werner, with your "procedures" above, It seems that I just need "input" a new function !  :

  Many thanks for all your time and help.
      Regards.