Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Can mathcad solf this
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can mathcad solf this
i am new to mathcad and want to know if mathcad can solf a quadratic system like this And know how many answers it gives.
2x1^2-x1+x2^2-3x2+4x3^2+5x3=53
x1^2+3x1-2x2^2+x2-2x3^2+x3=-17
-x1^2-3x1+2x2^2-4x2+x3^2-x3=2
THanks
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
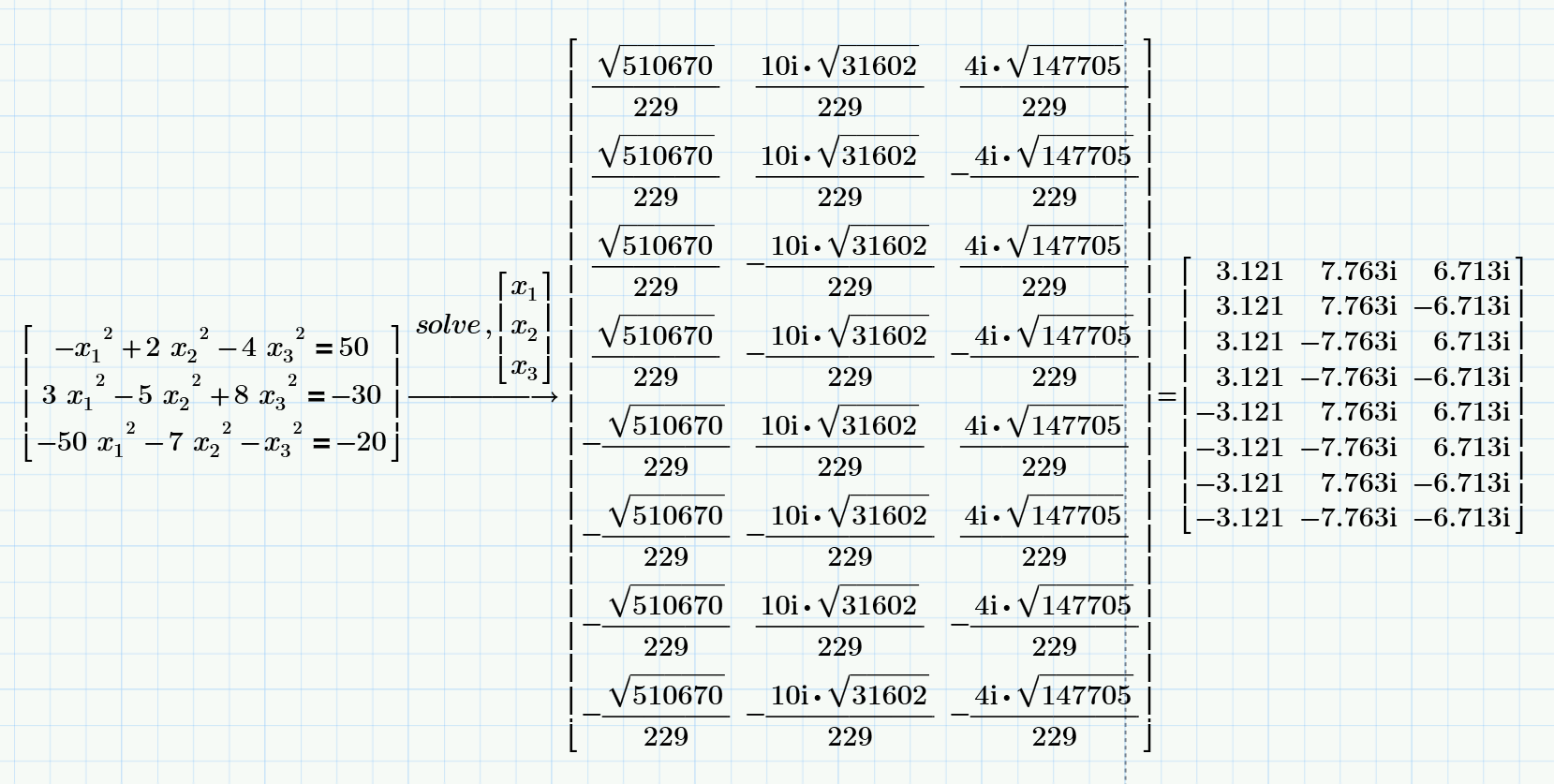
Try this but I think you must use a numerical not symbolic solution use (Find function)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can get two sets of real number solutions as follows (I've used M15):
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
On contrary to the example Valery posted in your system you have summands linear in x1, x2, x3, too.
This would mean that Mathcad has to solve a generic equation of eight order for which no general solution exists.
Therefore I guess the symbolic solver will fail and you have to resort to a numeric solve block which gives you just one solution triple depending on the guess values you have to provide. Different guesses may give you different solutions.
WE
EDIT: Looks like I was a bit late as Alan already solved the problem in an elegant way.
For completeness sake here are all eight solutions (just found by trying different guesses 😉

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
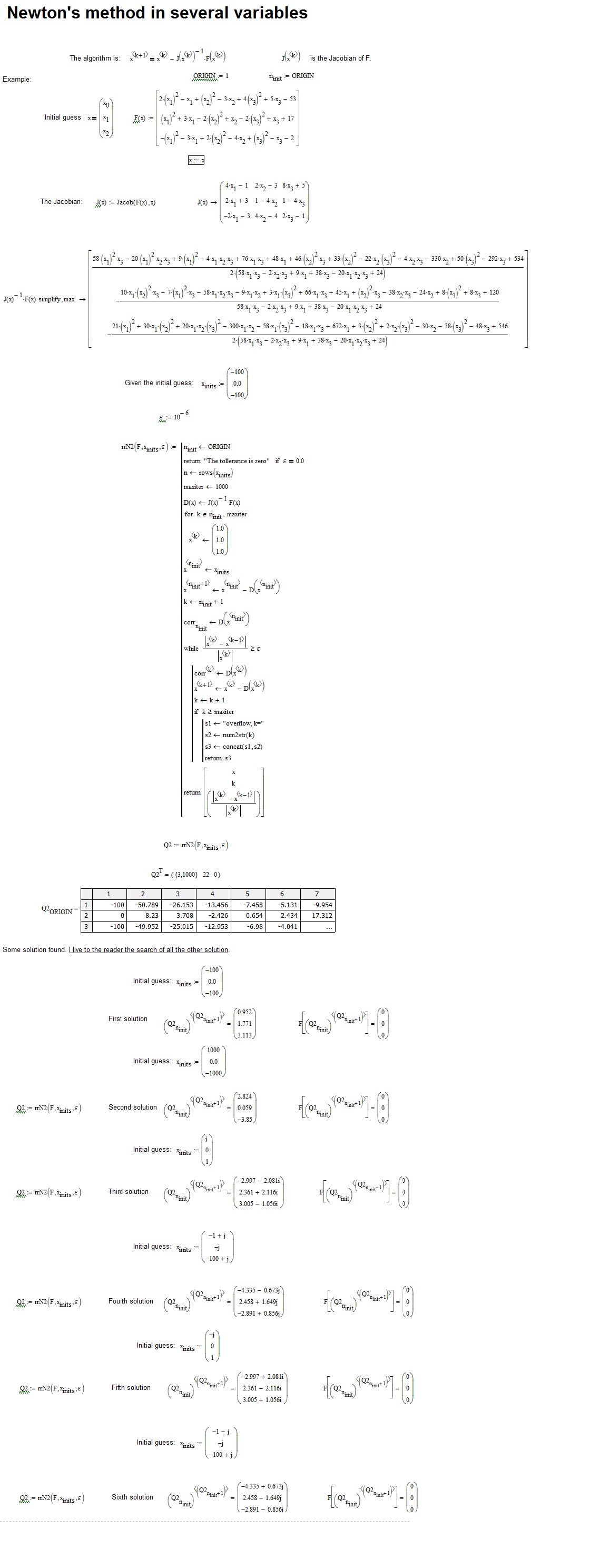
Hi Rob. If you like programming, you can solve your system in this way:


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The system has eight solutions (see above) not four.
Given that all coefficients are real, with any complex solution the conjugate is solution, too.
So you just missed the first set of complex solutions given in my answer above.
But probably Rob is interested in the two real solutions only anyway.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The method I adopted can be extended to find all 8 roots by making use of the function polyroots to find the roots of f(_z1).
ALan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The method I adopted can be extended to find all 8 roots by making use of the function polyroots to find the roots of f(_z1).
Combining symbolic solver and numeric methods that way sure is a clean, clever , sound way of solving that task. On of those "Why didn't I thought of that" things. I guess 😉
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I leave to the reader the task to search other solutions.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
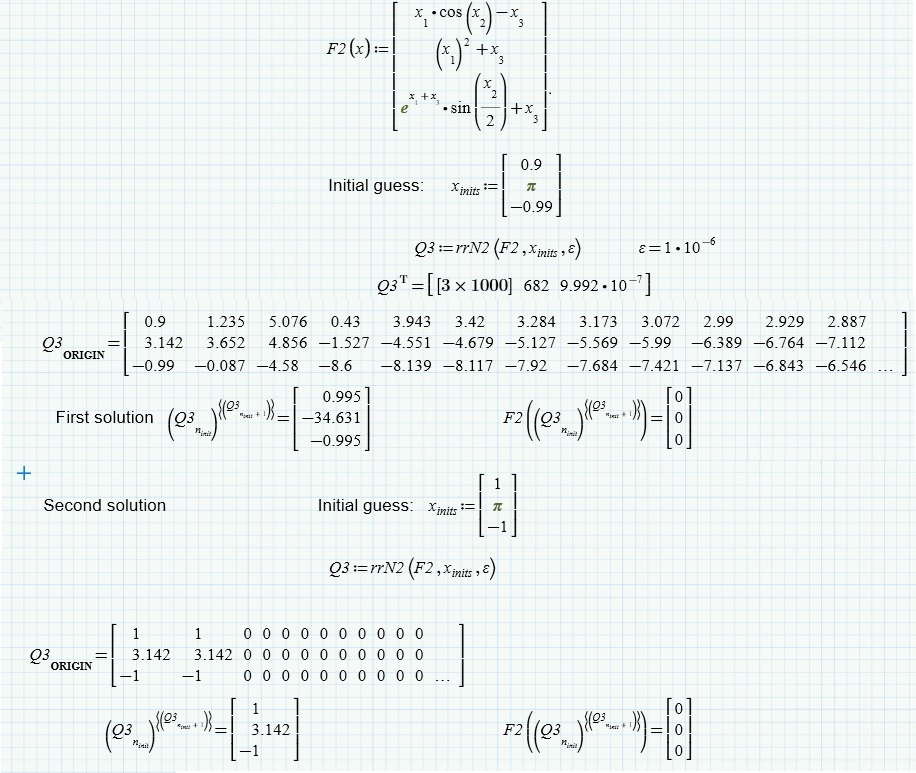
I would be pleased if you were also interested in another similar example in which the search of the roots is more difficult:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thank you





