ACCEPTED SOLUTION
Accepted Solutions
Okay.
- The 2 pi is the integral around the angle (full circle.) There is no dependence of radius (or height) with azimuth, so a true integral with angle is not required. (That's why there are only two integrals to get volume.)
- The variable "s" is a variable of integration. It does not appear outside the integral. The inner integral above is the integral over the radius. the limits of integration (for V3) are the radius of the center pipe (d/2) to the outside of the sphere (defined by the function r(z):
- The outside integral is the vertical integral (z), the limits of integration are the bottom and top of the water.
This is equivalent to your integral above except that the outer bound for radial integral is a function of height "rr(z).
Your integral has height as function of radius; I don't know how to write those functions.
Fred, I understand the integration of zylinders, etc.
But this is not the answer of my question.
I want to have the integration limits of the Integral concerning to the sketch:
This is a water-reservoir (shaded Area) of whitch i only want to know the integration limits for Integration to get the Volume.
Thank you
No Problem!
What is "s" in your formulas?
can you tell me the geometrical meaning of this?
It would be better for me to understand when you use the same parameter names whitch are given in the sketch.
Zylindrical koordinates:
Okay.
- The 2 pi is the integral around the angle (full circle.) There is no dependence of radius (or height) with azimuth, so a true integral with angle is not required. (That's why there are only two integrals to get volume.)
- The variable "s" is a variable of integration. It does not appear outside the integral. The inner integral above is the integral over the radius. the limits of integration (for V3) are the radius of the center pipe (d/2) to the outside of the sphere (defined by the function r(z):
- The outside integral is the vertical integral (z), the limits of integration are the bottom and top of the water.
This is equivalent to your integral above except that the outer bound for radial integral is a function of height "rr(z).
Your integral has height as function of radius; I don't know how to write those functions.
Thanks, now we get closer to the problem.
Can you please post your MathCad file?
Is rr (z) equal to z (r)?- it confuses me.
Inner limits are d/2 and r (z), is that right?
You solved my problem.
I guess i had the wrong sequence in the integrals.
First "r" then "z" and at last "phi"
The equation:
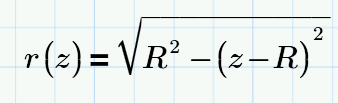
I can't see the geometrical meaning, can you please explain in a sketch?
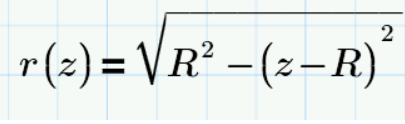
Solves for radius as a function of z, vertical position from the bottom of the sphere. (Pythagoras' Theorem.)
Height as a function of radius z(r) isn't helpful because there are two values of z for each r, while there is only one radius for each z.
The file is attached.
