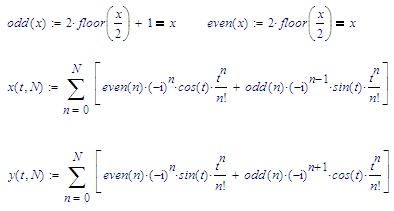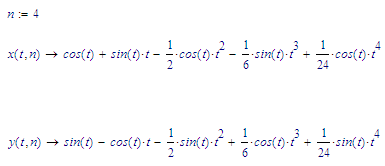Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Circle involutes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Circle involutes
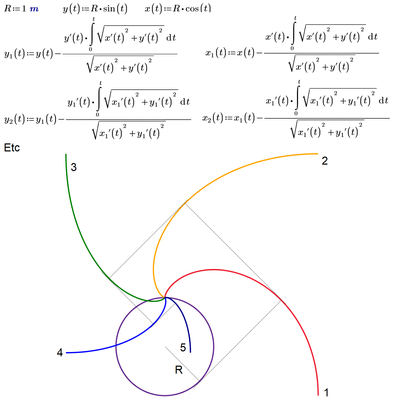
I am trying to build circle Involvents.
I built five involutes, and the sixth, the seventh, etc. there is not enough time and power of the computer - see attachment Prime 6.
I will be very grateful if you can give me a way to make my work.
- Labels:
-
Algebra_Geometry
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
how about:
It shouldn't be too hard to construct the next set from the previous. I see factorials in the coefficients to the various sine and cosine terms.
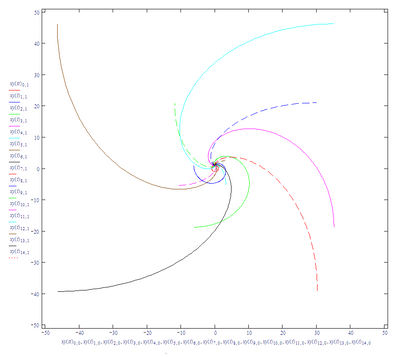
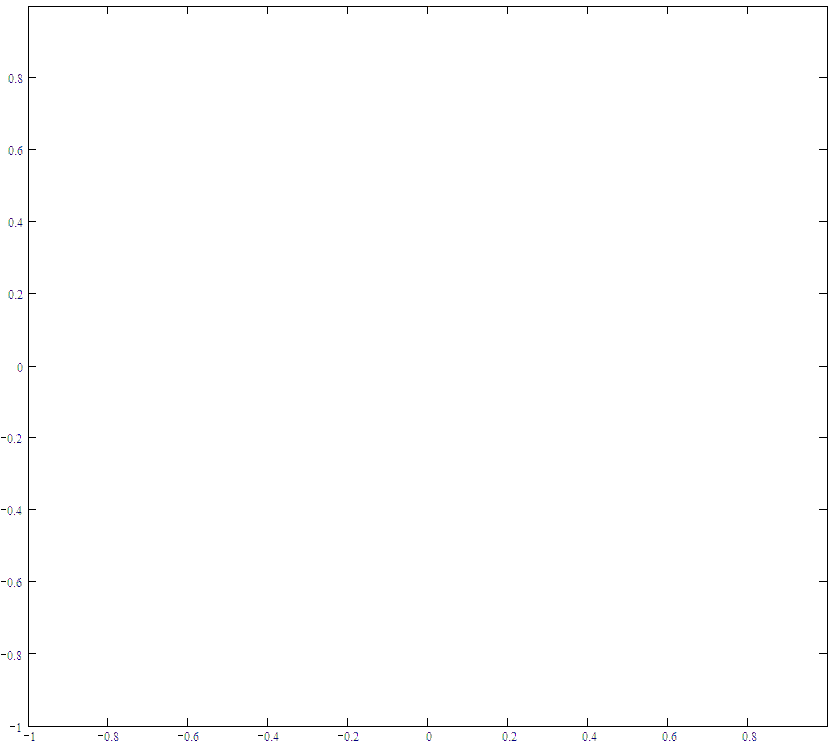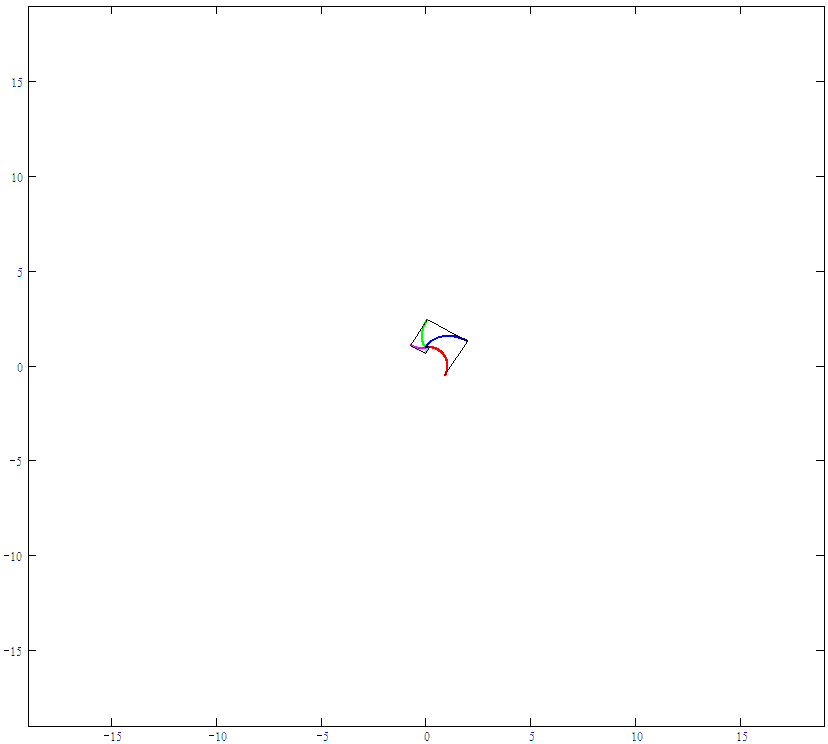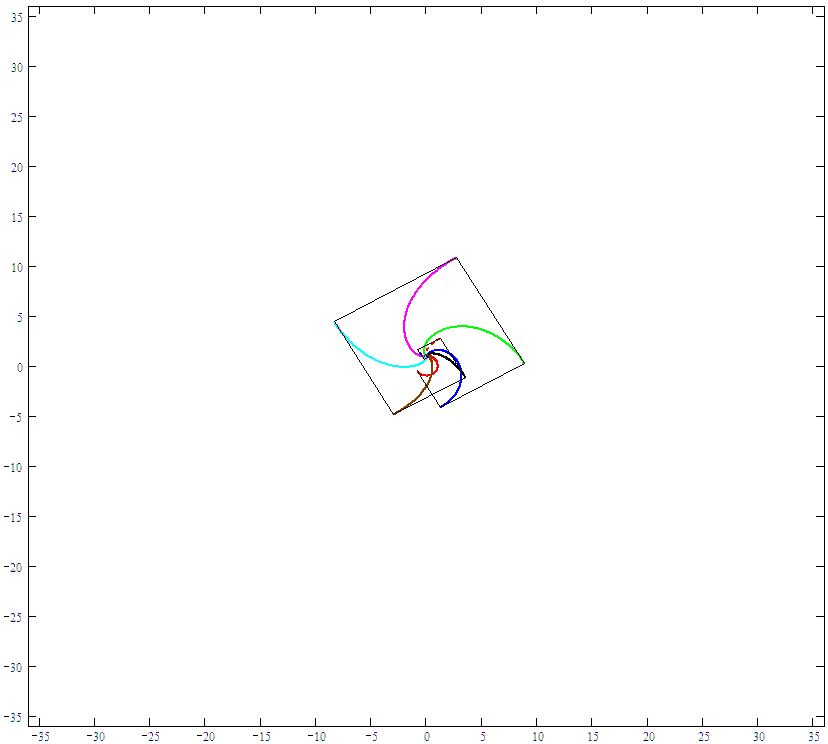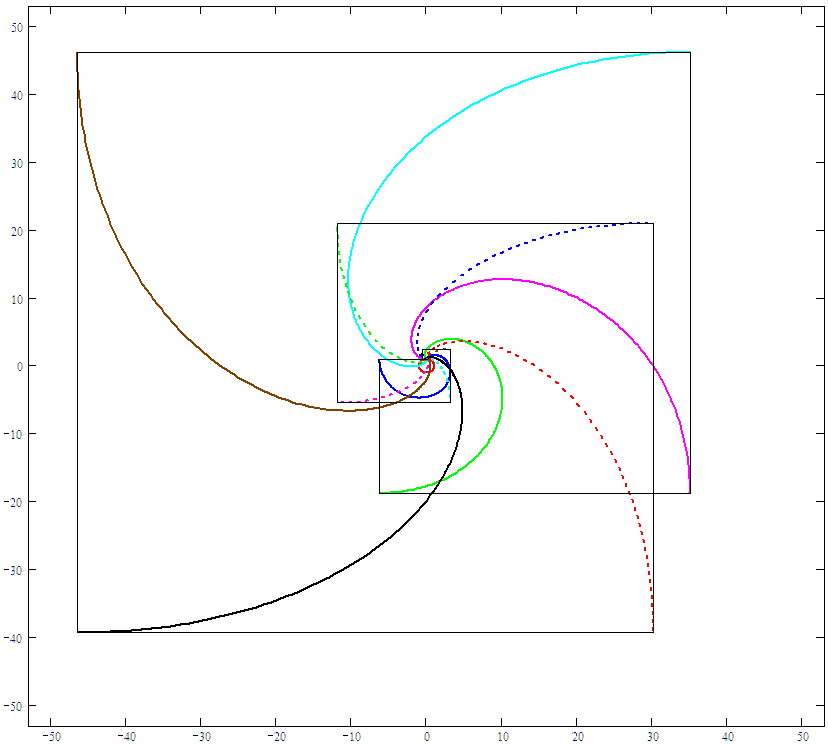
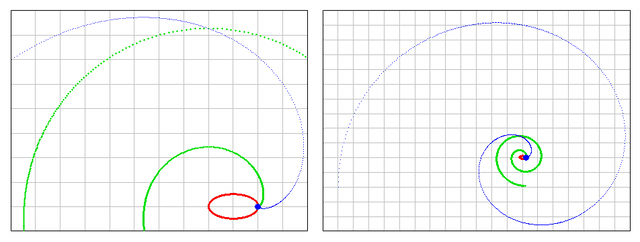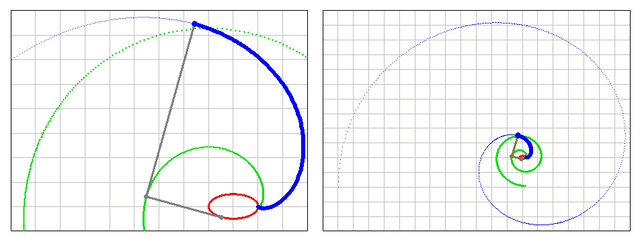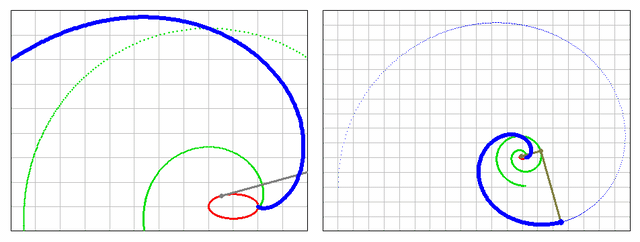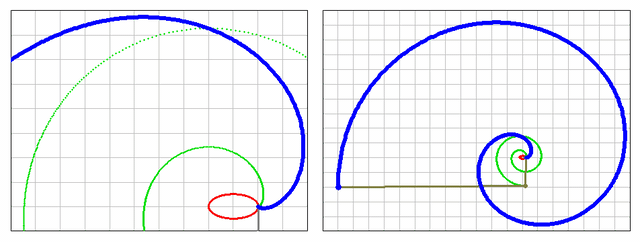
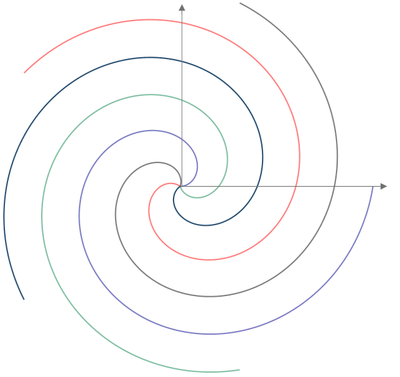
Here's the plot:
Note that the task gets much more complicated if you try to do this on an ellipse (e.g. leave y(t) as is, and change x(t) to 2*cos(t))...
Success!
luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Luc!
It is Mathcad 11 with old good Maple symbolocal engine!?
We must use the simplify operator in Prime 6.
Can you have more than seven involutes? Слабо?
With very interesting fractal!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Certainly.
This is the set of equations:
Here is the plot:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Found a better way to generate the symbolic expressions:
The sky is the limit...
or are we getting close to christmas?
@ValeryOchkov Maybe you get more results in Prime if you separate the integrand variable ( t ) from the integration limit ( also t ). As you can see, I've used tau instead of t for one of the two.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And of course there's an animation:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here are the generating functions for a set that starts with x(t)=cos(t) and y(t)=sin(t):
You get the first pair with:
the fourth:
and number 14:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may speed up calculations significantly if you use bold and simple numeric approximations for derivatives and integrals - working on vectors of points, not equations. Of course at the cost of accuracy (especially with higher "order" evolvents).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
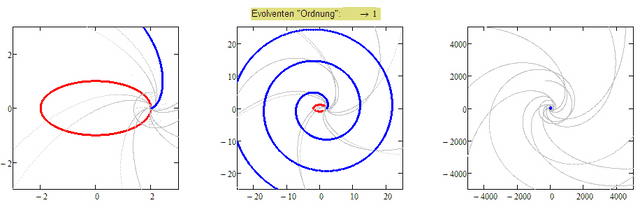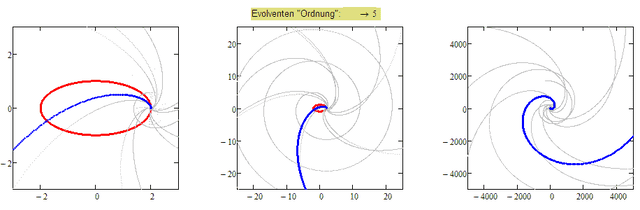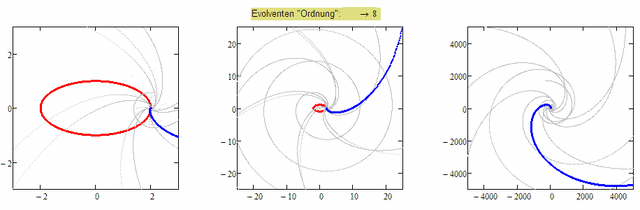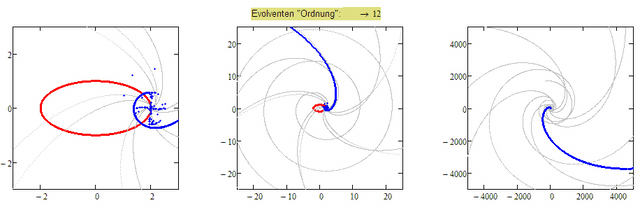
Here is a first try with a numerical approach working on vectors. Its not really satisfying with other base curves, but works OK for curves like ellipses (unless the "order" gets too high). Here is the first dozen from the ellipse suggested by Luc:
Here's the construction of the first two:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fine, Werner! Solution without atimation is not solution!
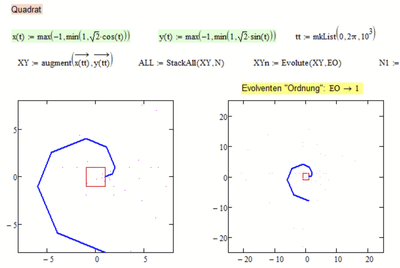
And what about a square not a cyrcle or an ellipes?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Fine, Werner! Solution without atimation is not solution!
So why are you using Prime, if you like animations?
And what about a square not a cyrcle or an ellipes?
Sure! 😄
See my other post with the file attached which you now can change at will 😉
You sure will have to put some work into it as it doesn't work OK out of the box as you can see here:
EDIT: And of course you would have to define first, how you'd like to define an "evolvente" (of a straight line). Normal definition wouldn't apply 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Forgot to attach the file and the forum software didn't let me edit my old post, so its attached here.
As you may notice a lot of crazy artefacts are created for higher order evolvents (thats the reason I used "points" and not "line" for drawing). Guess this could be because of the bold numerical derivative and maybe could be improved. Its also dependent on the number of points created - the higher the number, the sooner we see strange effects. So maybe some errors are cumulating.
Furthermore the approach fails if the base curve has an apex (a point with zero curvature). In the file you find some examples like semicubical parabola (Neile parabola), astroid, catenary, cycloid).
If the problems could be fixed it would be necessary to make the starting point selectable (at the time its the first point in the data set) or (maybe as an alternative) make the initial lenght of the tangent selectable.
I don't think I will find the time to fix the file so I attach it here in MC11 format - maybe someone would like to take a closer look at it. Have fun!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It appears you try to divide by zero, so that is going to take a little while to solve. Attached is probably no help for what you're trying to do (which I'm not sure of), but it's a little tool I've used for gear teeth.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
is it possible to creat someone so: involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute - involute-evolute...