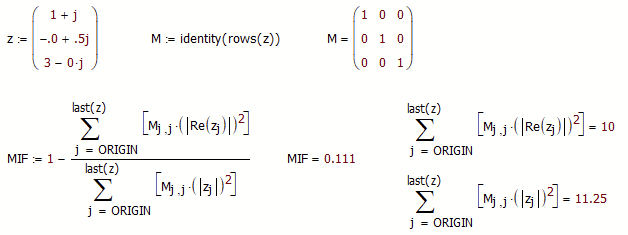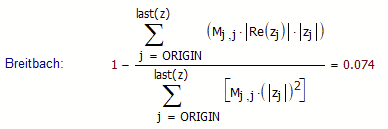Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Clarification of a formula for MIF
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Clarification of a formula for MIF
To all
I am dealing with a formula and I am hoping that the more mathematically inclined among you might be able to clarify something for me.
On the attached mcad 15 file there is a formula for a mode indicator function. I am still trying to source the original reference but in the meantime I thought I ask the question.
Could anyone tell me how the sum on the numerator works? Is the formula saying that one has to sum over the entire vector?
Thanks in advance
Regards
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
-
Mechanical_Engineering
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would see it that way
Actually the absolute value in the nominator isn't necessary as here a real number is squared.
Using vectorization you could also code it in Mathcad like this
The other formula (Breitbach) yields a different result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would see it that way
Actually the absolute value in the nominator isn't necessary as here a real number is squared.
Using vectorization you could also code it in Mathcad like this
The other formula (Breitbach) yields a different result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the input. I cannot find any paper/text, etc from the quoted "reference". Never mind
The formula yields 1 number. In reality the complex vector is frequency dependant. That is each row is a value at a given frequency
If I got this right if an entry in the complex vector is (near) to imaginary then the MIF should drop (close to zero, drop to a minimum) (at a given frequency)
So one should be able to plot a MIF value at each frequency
Anyway you have answered my original question
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@JXBWk wrote:
Thanks for the input. I cannot find any paper/text, etc from the quoted "reference". Never mind
Would this help
https://pdfcoffee.com/ecss-e-st-32-11c31july2008-pdf-free.html
See 3.2.33
Maybe this paper can be of help, Formula (6) seems to correspond
http://papers.vibetech.com/Paper35-MMIF.pdf
But I have to state that I'm way outside my comfort zone here and have no knowledge of the underlying subject matter.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes that's where the formula I pasted in the mcad file is coming - the ecss reference. This one yields 1 number
The 2nd ref I am have and is for the Multivariate MIF - uses the H matrix and is an eigenvalue problem ? (or maybe I am confuses with the Complex MIF (CMIF) !)
of interest: 546802.pdf (hindawi.com)
equation 8