Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Comparing Two RV Arrays and Outputting Character Strings
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Comparing Two RV Arrays and Outputting Character Strings
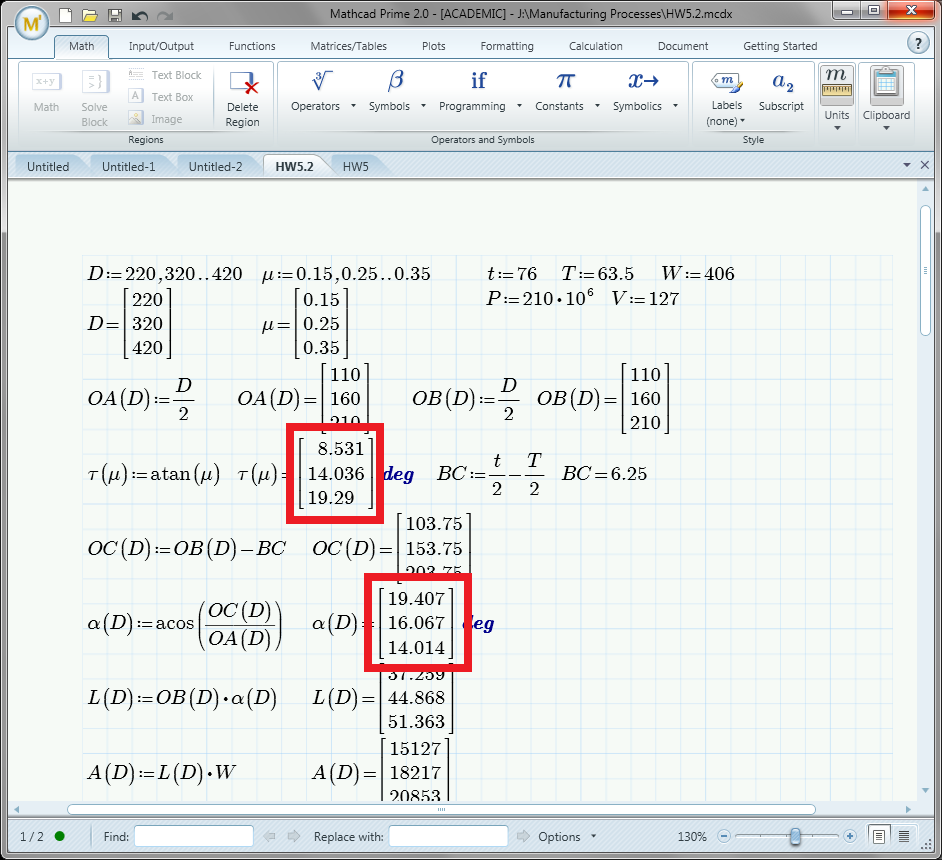
So I'm very new to mathcad prime and I'm trying to compare resultant numbers from computing with range variables. I was hoping someone could show me how to figure out what I'm trying to accomplish.
Example (simplified):
I've defined two range variables
A:=220,320..420
B:=840,640...440
then applying some math with the RVs
C(A):=A/2
D(B):=B/4
I would then like to compare the first value of C to the three values in D and determine if it is greater than or less then the D value and then output an array with Yes if greater, or No is less than. Then repeat this with the second and third values in C respectively.
I'm thing something like this...
i=0
j=0
for i=1:3
for j=1:3
if C(i)>D(j)
E(i+j) = "Yes" %I'd like the ouput to be a one dimensional array/vector and not a two dimensional matrix
else
E(i+j) = "No"
end
end
The red boxes are the two variables I'd like to compare, and display if alpha is greater than tau in a coulmn matrix/array.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The attached should help. Be careful to learn the difference between range variables and "proper" variables.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would you be so kind as to briefly describe the difference?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See the attached articles by Stuart Bruff.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Btw, thank you very much for the file. We're using Mathcad 15 in my Manufacturing class and my teacher is barely explaining it, and assumes we've used it a bit in other classes (while I have not). So I'm thanks the liberity to teach myself Mathcad Prime 2.0 since it's newer and available. The program is very powerful, and while my teacher wants us to compare the two angles by hand and write yes or no on a seperate sheet of paper, I figured I'd learn how to do it in Mathcad since it's possible with the programming tab anyway.
I was trying to take my Matlab experience and apply here, but was just having a lot of trouble.
Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Matthew,
The following video tutorials for Mathcad Prime can help you learn the program:
http://learningexchange.ptc.com/tutorials/by_sub_product/ptc-mathcad-prime/sub_product_id:19
And also this tutorials (you can find them in attachment too):
http://www.ptc.com/company/community/schools/projects.htm#mathcad-prime
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
By changing the D and mu RVs to Matrices it has complicated/messed up later computations
D:=220,320,420
mu:0.15,0.25..0.35
So if where to to multiply D*mu, it now returns a singular number from the dot product. But I want it to return 3 individual numbers like before.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Matthew Machart wrote:
By changing the D and mu RVs to Matrices it has complicated/messed up later computations
D:=220,320,420
mu:0.15,0.25..0.35
So if where to to multiply D*mu, it now returns a singular number from the dot product. But I want it to return 3 individual numbers like before.
This is what vectorizing is for. If you do not want D*mu be interpreted as dot product but want the multiplication be iterated over the elelemnts of both vectors, you have to vectorize that product. You can use the Matrix toolbox or use the keyboard shortcut "Ctrl & -" to do so.
Sorry - just saw that you ar using Prime. Keyboard shortcuts are language specific here. By trial and error (the docs are wrong) I found that its Strg-Alt-6 for me. Use the the operators menu in the calculate ribbon.
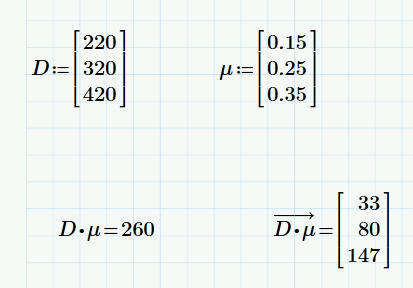
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
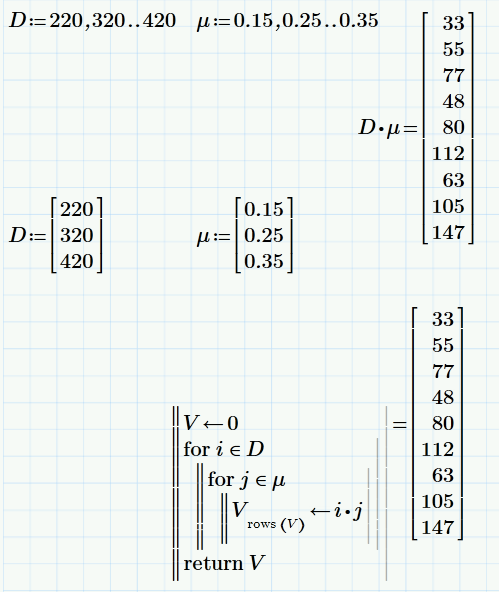
Oh....T_T that's easier... I did for loops instead for everytime i had to multiply lol.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Matthew Machart wrote:
Oh....T_T that's easier... I did for loops instead for everytime i had to multiply lol.
Yes, but to duplicate the behaviour of the product of two range variables (which you should not use for that kind of calculations anyway) you would have to resort to loops. The results may look alike but they aren't. The latter being a full fledged vector you can reuse in a predictable way.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well this the final product I have as of now (see attached). Any recommendations on how to improve what I've done.
PS: I'm learning a lot from this and thuroughly enjoying it. Thanks everyone for your input!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I noticed that you did not use any function but evaluated all "on the spot". Using function can be convenient in most situations and is more versatile.
I showed it as an an example with the last table. See attached





