Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Conformal Mapping in MATHCAD PRIME
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Conformal Mapping in MATHCAD PRIME
Good evening.
I would like to implement a MATHCAD PRIME worksheet to map a solution on a circle to another domain. This technique is well known as conformal transformation. However, I tried to solve it numerically without success. I use this to predict the potential flow pressures around a body in 2D. Does anyone knows if this problem has already beel solved and indicating in which thread? I tried with the search function on the website, but no results. Thanks in advance for the support.
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
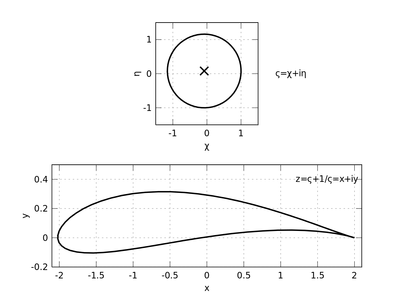
Which kind of conformal map function do you have in mind? f(z):=1/z or inversion (f(z)=1/conjugate z).
Here is a quick hack. The mapping is done point by point, not analytically.
You may chose your own mapping function.
Hope it helps.
Prime10 file attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which kind of conformal map function do you have in mind? f(z):=1/z or inversion (f(z)=1/conjugate z).
Here is a quick hack. The mapping is done point by point, not analytically.
You may chose your own mapping function.
Hope it helps.
Prime10 file attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good night Werner.
Thanks for the mapping solution. Unfortunately the domain I need to map into a unit circle is not described with a function, but by points. I am talking about a wing section.
I think that if I provide a vector of value your algorithm should work. Am I correct in my understanding?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@gianfry wrote:
Good night Werner.
Thanks for the mapping solution. Unfortunately the domain I need to map into a unit circle is not described with a function, but by points. I am talking about a wing section.
I think that if I provide a vector of value your algorithm should work. Am I correct in my understanding?
As long as the mapping is done by a function this should work.
Actually my approach only works with a matrix of point coordinates - n x 2 matrix, first column x-coordinates, second column y-coordinates. The result of my function is a similar matrix with the coordinated of the mapped points.
I used an explicit function (the sinus) and the parametric equation of an epicycloid just for demonstration. It was necessary to sample x- and y-values anyway so that my function could do its job. So if thats the data structure you have right from the start it should be OK.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good evening, Werner.
Following your spreadsheet I finally was able to get the transformation I was looking for. Of course it is based on a function. Now I am working on the implementation of a mapping for a general shape into a unit circle, when the mapping function is not known. I found a paper from Theodorsen, dealing with such a type of problems, but before doing that I am working on plotting stremlines of a potential flow around this type of profile. The solution is well known...I need to figure it out numerically.
Thanks again.
Regards,
Gianfranco
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good evening, Werner.
The MATHCAD file attached is the updated version of the previous one, with the potential flow and pressure distribution solved over a Joukowsky airfoil through the conformal mapping technique. Since this solution is exact, it is used to validate numerical methods trying to solve the same problem, like the panel methods.
Maybe it will be useful for other colleagues to have a MATHCAD example to start with and it is my way to say thanks to the community.
Of course, should anyone see improvements, feel free to suggest.
Regards,
Gianfranco