Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Creating the “enveloping” ellipse for a Monte Carlo plot?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Creating the “enveloping” ellipse for a Monte Carlo plot?
To all
I am doing my 1st step with the montecarlo() function in mcad 15. I copied the example and put my own function and it seems to work fine.
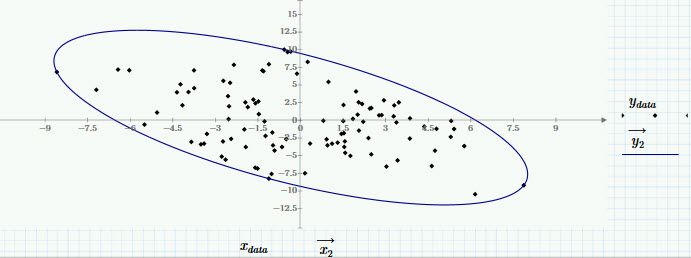
Does anyone know if there is a way of getting/creating the “enveloping” ellipse one often sees on a Monte Carlo plot? I attached one on which I drew the ellipse
I think the length of the minor and major axis have a meaning (in the Mont Carlo world) byut can’t quite remember what it is!
Solved! Go to Solution.
- Labels:
-
Programming
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Get the mean data X0 =(x0,y0)
Get pts
1: X1=(x1,y1) x1=min(x), y(x1)
2: X2=(x2,y2) x2=max(x), y(x2)
Centre of the ellipse is X0
Major axis a =|| X2-X1||
Rotation angle of the ellipse atan(|X2|/|X1|)
Search minor axis (b) to envelope all the pts
Plot ellipse translated by X0 and rotated by alpha
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Get the mean data X0 =(x0,y0)
Get pts
1: X1=(x1,y1) x1=min(x), y(x1)
2: X2=(x2,y2) x2=max(x), y(x2)
Centre of the ellipse is X0
Major axis a =|| X2-X1||
Rotation angle of the ellipse atan(|X2|/|X1|)
Search minor axis (b) to envelope all the pts
Plot ellipse translated by X0 and rotated by alpha
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And the minor axis is?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Haven’t quite work this out in detail – I thought I had something !
I know that it is a vector normal to a =|| X2-X1|| and must be of such length as to enclosed all (most) of the points
Some of steps work fine in a stand-alone example but not when I try to integrate it to the monte-carlo plot
So kind of a step back !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about this?
You've calculated the angle for the major axis. (I liked what you've got so far.
Now
Rotate all of the data so that the major axis is parallel to the x axis.
Then the length of the minor axis is max(y)-min(y). And the minor axis is normal to the major axis, so you know the whole ellipse.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Indeed
so I need to rotate each pair of data (from the data set from the montcarlo output)
data=augment(hv,R)
(where hv is the variable and R1 the output of the montcarlo)
if Rz is the rotation matrix (anticlockwise)
datarotate=(Rz(-beta)*data^T)^T
where beta is the angle for the major axis
Cannot plot this ! so must work on each set of data
Working on a cut-down version of the test sheet to post
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks
Why is there no way of rotating the "scatter" data M(x,y) using a rotation matrix?
Mrot(x',y') = R(alpha).M(x',y')
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@JBlackhole wrote:
Thanks
Why is there no way of rotating the "scatter" data M(x,y) using a rotation matrix?
Mrot(x',y') = R(alpha).M(x',y')
There is; you'd need to have the data paired (x,y) rather than two separate vectors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a solution that uses Minimize to make an ellipse of minimum area that includes all the points. Seems to work.
4.0/pdf attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for that.
Thanks to Fred and yourself for the input. Really appreciated
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
VERY NICE!!