Curve and surface fitting

[erguezga]

Hi,

I have several series of points (x, y) and I have fitted each series in an exponential curve using expfit function.

Each series of x and y points has the same z.

Now, what I am trying to do is getting a general equation (x, y, z)  to relate x, y and z in one equation.

I tried to create a surface with CreateMesh (using regress and interp with all the points, not the fitted curves) but it seems that I do not have access to the equation which links the points. Is it possible to get an equation of the surface?

I tried to do something with the fitted curves instead of the raw points but I have not found how to do it. s there a function in Mathcad 15 to do that?

I am attaching two files with the fitted curves and the surface created.

Could anyone help me?

Thanks in advance

[Fred_Kohlhepp]

For problems were a polynomial fit is acceptable, regress works to create a surface fit.

[Werner_E · Accepted solution]

So your question is, how to get a look at the equations itself, right?

If you are happy with the polynomial approximation of second order you did in your file with regress, its easy to get the equation because the 6 coefficients are part of the vector vs you create using "regress".

If you look at the help for regress you will find a link to a quicksheet at the end of the text. This quicksheet tells you, how to extract the correct coefficients.

In your case (2 variables and order 2) you may do like this:

[erguezga]

Thanks!

Is there a way to use an exponential fit instead of a polynomial one in 3D?

[Werner_E]

Enrique Rodriguez Garcia wrote:

Thanks!

Is there a way to use an exponential fit instead of a polynomial one in 3D?

Not out of the box as we have it for 2D, but you can always set up your desired function, define the residuals and minize them using the "minerr"  function.

Which 3D-function du you have in mind when you say "exponential fit" in 3D?

[erguezga]

The problem is that the surface does not fit very good so I was searching something similar to what I did in 2d for every set of points with the same z value using the expfit function so, what I wanted to obtain is an equation which contour plot were something similar to this (only half of the previous surface with the symmetry axis in y=90):

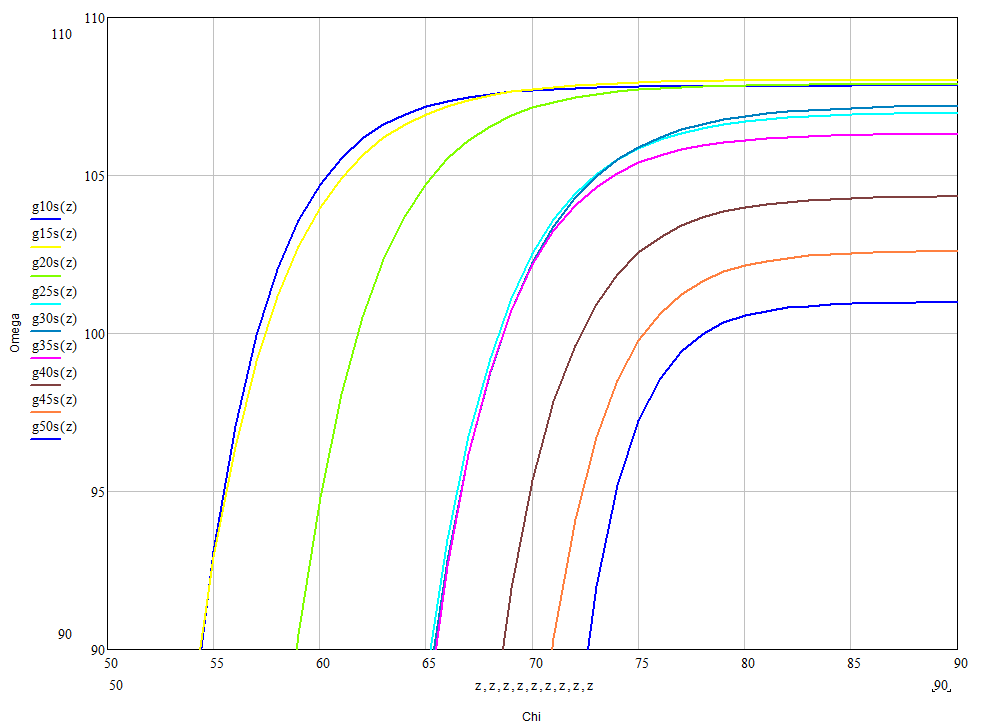
In order to set up the desired function, should I use genfit or is there another one to do this?

Thanks for your help!

[Werner_E]

As far as I am aware you can't use genfit for a 3D function z=f(x,y). Simply use minerr.

But first you would have to decide which type of function you want to give a try. Then you can try to find its coefficients using genfit.