Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
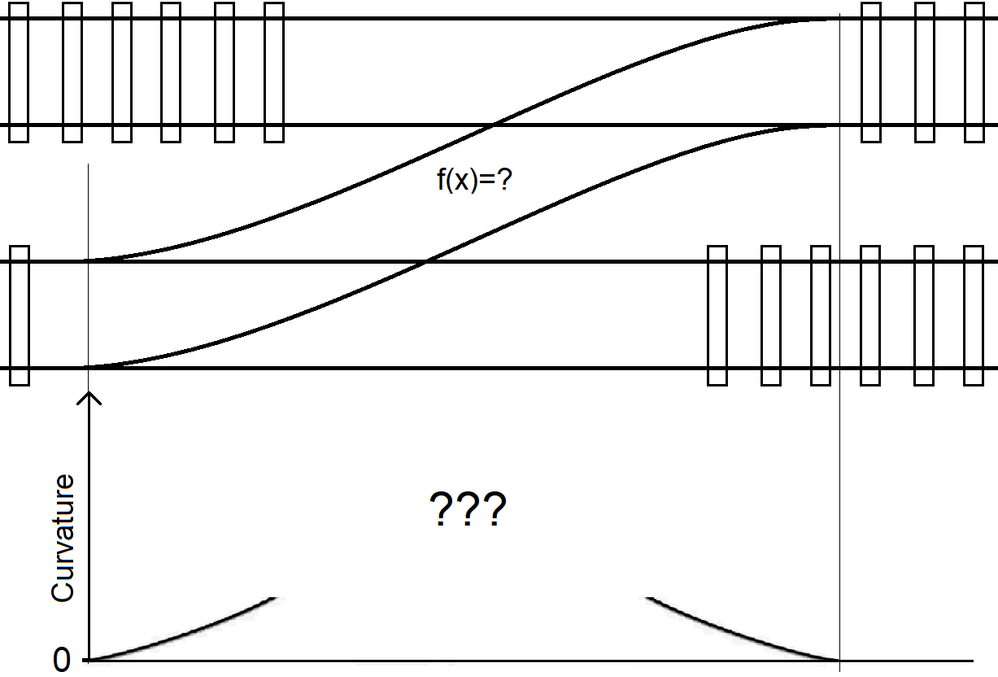
Curve for switch transition
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Curve for switch transition
What do you think the curve should be f(x).
See please this too https://community.ptc.com/t5/Mathcad/Euler-spiral/m-p/912205#
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would treat it like a cam, One key feature would be to avoid infinite jerk (rate of change of acceleration). I've read that that makes for a more pleasant experience for the passengers (or cargo). There are many cam profiles that can do that. You'd want to balance jerk, acceleration and sideways velocity. I'd start with 3-4-5 poly or cycloidal cam profiles, but I like to think the industry standardized on one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
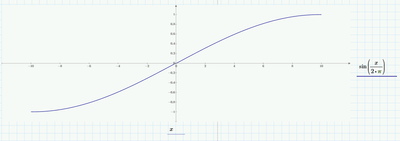
Your sketch of the track's transition (zero slope at each end) looks like a simple sine wave to me!
Cheers!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ChrisKaswer wrote:
Your sketch of the track's transition (zero slope at each end) looks like a simple sine wave to me!
Cheers!
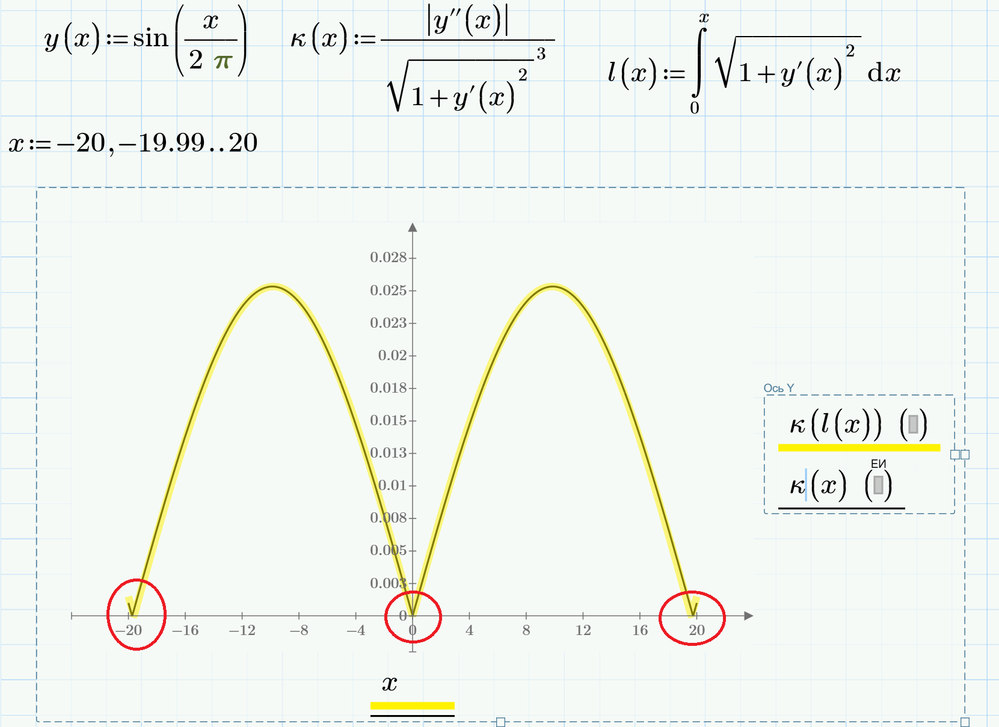
What can you say about this solution?
I specify the type of curvature of the curve (sine for example) and numerically solve a second-order differential equation - a boundary problem:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
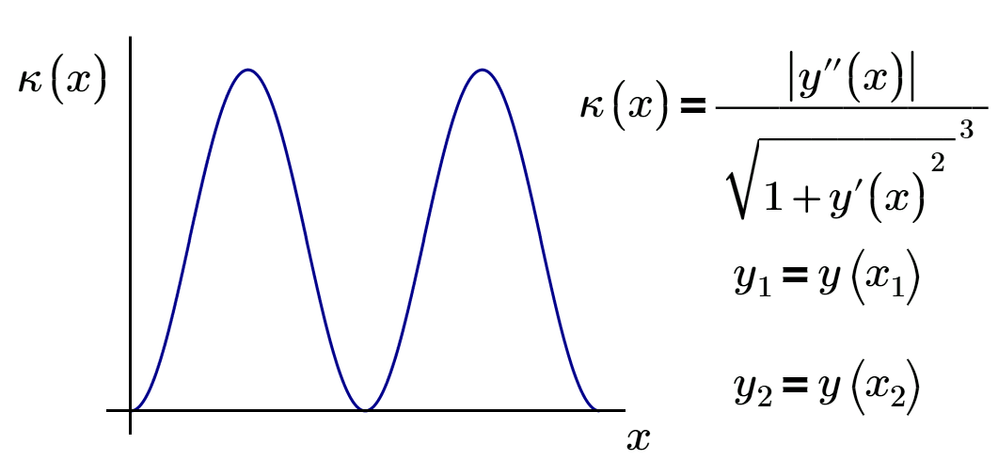
Paying attention not only to curvature but also to the third derivative of the displacement ("jerk") is certainly not unimportant, but let's not forget the fourth derivative ("snap" or "jounce"), the fifth derivative ("crackle") and the sixth ("pop"). 😄
The requirements for railroad tracks with lateral acceleration, wheel-rail friction, etc. are certainly completely different from those for road construction, where you could perhaps model with one (or two congruent) clothoid(s).
By the way, you're not just dealing with a single function here! If f(x) describes the fictitious center line, then the rails are so-called parallel curves and these are usually more complex different functions.
If you take this problem seriously, you can certainly have a lot of "fun" with it for a very long time ...
You may also be interested in this paper (in German),
https://dgk.badw.de/fileadmin/user_upload/Files/DGK/docs/b-314.pdf
in which the course of the rail is modeled by various different function types and also spatially because the rail inclination, which is intended to compensate for the lateral acceleration, is also taken into account.
However, I have only briefly skimmed the pamphlet...