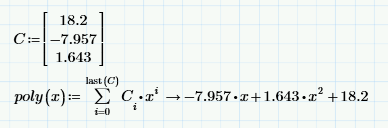Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Defining a Curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Defining a Curve
Hello to all,
I am interested to know if it is possible to mathmatically define a curve as a function. i.e. if I have an xy plot which I have created a curve for i.e. a polyfit or similar. Is it then possible to get MathCAD to define that plot as a function of x? i.e. if I have a polyfit line (which I understand to essentialy be an extrapolation of the xy plots themselves) can this polyfit line be defined as a function i.e. y(x)?
Thanks,
Andy
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
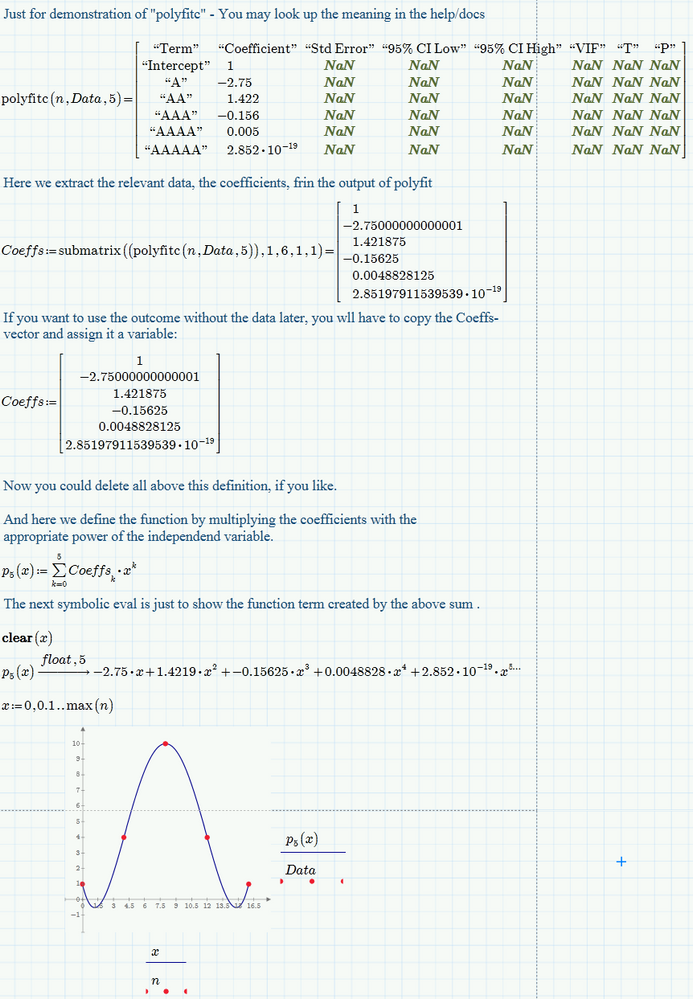
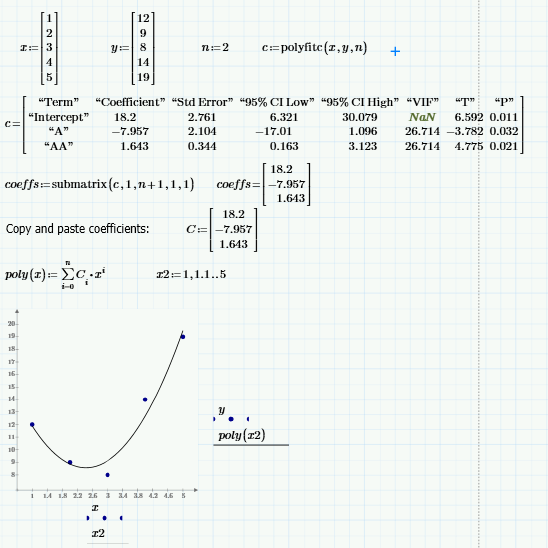
Here is a sheet in Prime 3.0 format.
Hope it helps.
To use the function without the data availabe you would copy simply the "coeffs" vector (set Prime to show more decimals for better precision) and assign it a variable "coeffs" which you then can use for the function definition as shown.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
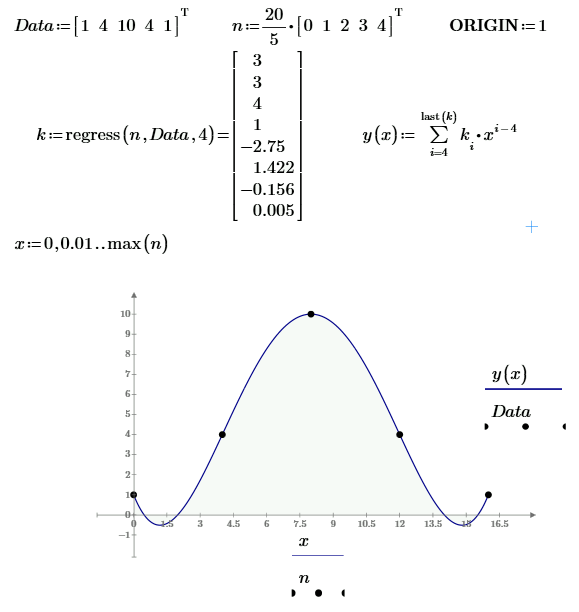
The regress function returns coefficients of the polinomal for the approximation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Any advice on how that works?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here you go:
Next, see what happens if you change the value of order..
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure this is quite what I am after.
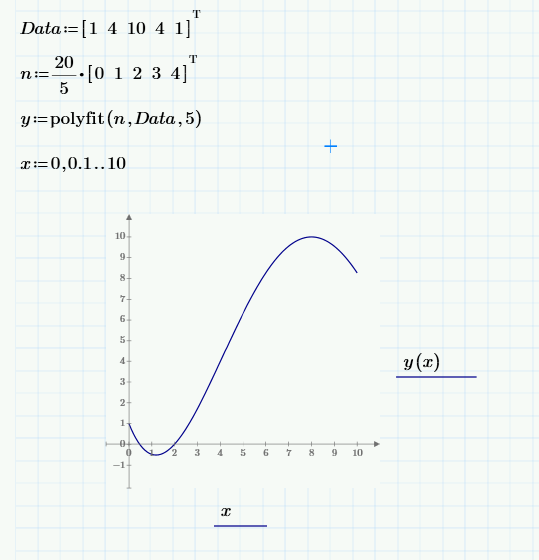
Say for example I have a series of data and I fit a curve to this as in the attached. What I am now interested in doing is expressing the produced curve as a function of x so that I could not plot the curve without the need to reproduce the data and could simply plot the function. Is this possible?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That is why you use the regress function. It provides the coefficients of the polynome:
you can write myf(x)=a*x^2+b*x+c with a=-0.357, b=1.643 and c=2.
Sucess!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Any chance you can show me how that might work in my example?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
Any chance you can show me how that might work in my example?
Send please your example! As Mathcad-sheet!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
Say for example I have a series of data and I fit a curve to this as in the attached. What I am now interested in doing is expressing the produced curve as a function of x so that I could not plot the curve without the need to reproduce the data and could simply plot the function. Is this possible?
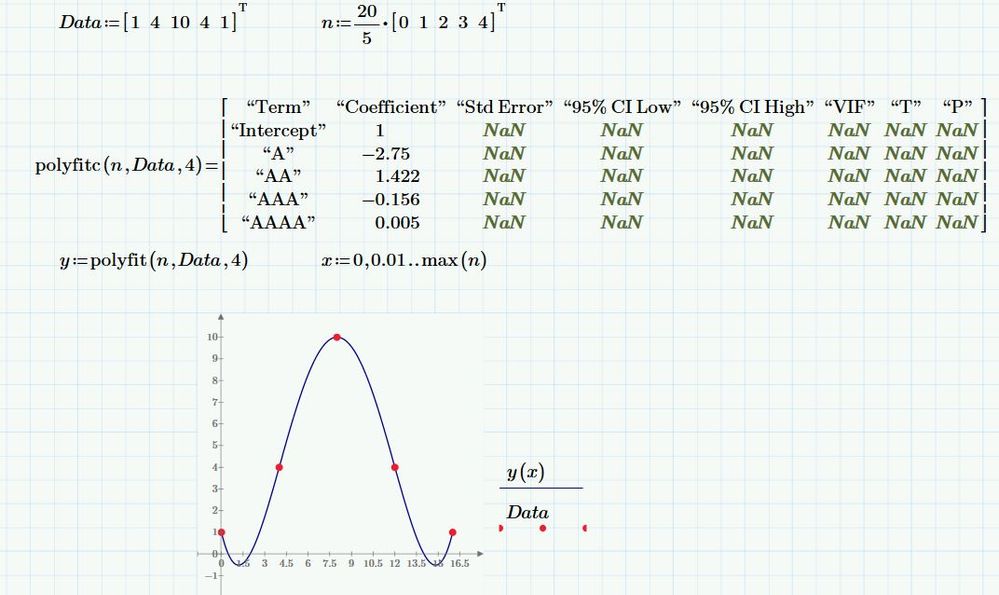
Not using polyfit, no. Use polyfitc instead (which replaces regress) to return the coefficients of the polynomial, then use the coefficients to define a function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Can you show me an example?
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure I am explaining myself. In this outcome you are not left with a function that you could then take to a different worksheet and input to recreate the same curve. here, whilst you have y(x) you have had to define this yourself as opposed to this being derived and is dependant on the other information in the worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Good to hear from you. In the example above I see that here you are given the coefficients of y in terms of x (or at least that is what I think has happened). How easy is this to take and put into a function that could be reporduced in a different mathcad file?
Cheers,
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In addition to what Richard has shown, you can also symbolically evaluate the equation poly(x). This will show you the exact equation being plotted.
Edit: example
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I only have MC Prime 3 any chance you can save in an older file format? I am not seeing how you have created x-1 under the Sigma notation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
I only have MC Prime 3 any chance you can save in an older file format? I am not seeing how you have created x-1 under the Sigma notation.
It's not possible to back-save to older version in Prime.
What x-1 are you talking about? I'm not seeing x-1 in any of the examples given.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a sheet in Prime 3.0 format.
Hope it helps.
To use the function without the data availabe you would copy simply the "coeffs" vector (set Prime to show more decimals for better precision) and assign it a variable "coeffs" which you then can use for the function definition as shown.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks everyone I think I have what I was after now! Thanks for taking the time!.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just leading on from this I have been playing with this again with the most simple of excercised i.e. x=y in the attached. This does work (providing the coefficients are accurate enough i.e. have enough decimals) but I was looking to see if MC can tell you what function the line/ curve is. i.e. in this case you would expect the result x=y or y(x)=x. I guess this is not acheiveble?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No, Mathcad cannot do that. Neither can any other software. There are an infinite number of curves that would fit any data to within acceptable tolerances, so without other information it is not possible to know what "the" curve is.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
Just leading on from this I have been playing with this again with the most simple of excercised i.e. x=y in the attached.
I can't see any attachment.
I was looking to see if MC can tell you what function the line/ curve is. i.e. in this case you would expect the result x=y or y(x)=x. I guess this is not acheiveble?
Your guess is correct. As Richard already explained, thats a mission impossible.
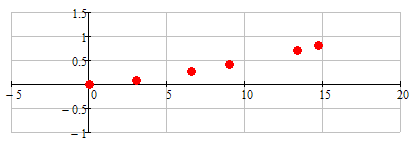
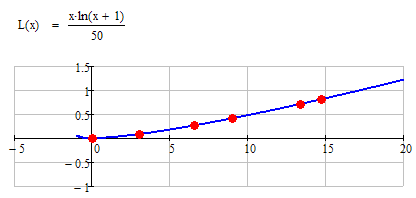
When you see this, what would you think, the equation of the underlying function is?
Perhaps we have here a linear process with a few inaccurate measurement results?
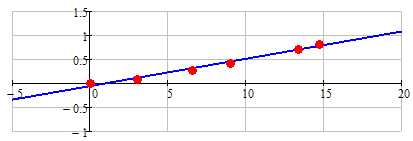
Lets reveal the secret - I used the function equation seen in the picture
You may say, that the straight line above wasn't a perfect match anyway - thats correct.
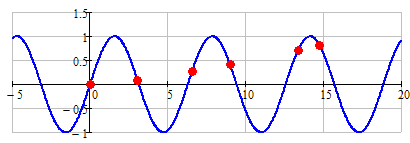
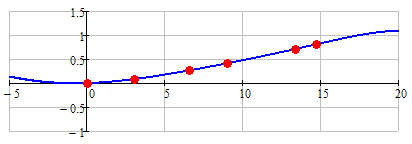
But here are two perfect matches - all six points lie exactly on the curves.
Here we have y=sin(x):
And here is a polynomial of sixth order:
And there sure is an infinite number of other function which include those six points perfectly.
So what should Mathcad return? 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
An interesting, although somewhat irrelevant, thing about the number of possible curves in space is that although there is an infinite number of them, and there is also an infinite number of rational numbers, it can be proven that there are more possible curves in space than there are rational numbers. It can also be proven that although there is an infinite number of integers, there are more rational numbers (this is in fact quite easy to prove). aleph two, aleph one, and aleph zero ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I intentionally duplicated Val's number to illustrate that polyfitc and regress will create the same numbers. Richard showed that you can "cut them out," and copy them from one worksheet to another, and the same function definition (from Val or Richard) will develop the polynomial as a function.