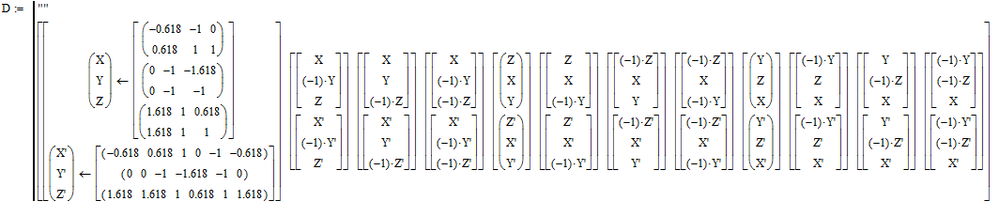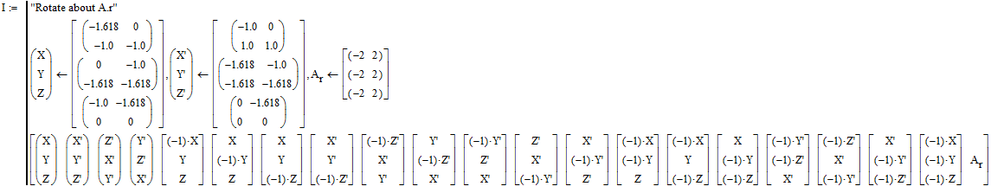Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Divide a surface into equal sized areas
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Divide a surface into equal sized areas
Puzzle only to fun. Question graphs are made by using Mathcad programing.
Divide a surface into two equal sized areas by using matchsticks.
1. With using two matchsticks.
2. With using three matchsticks.
3. With using n>3 matchsticks.
Solved! Go to Solution.
- Labels:
-
Puzzles Games
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's a no-brainer. I have very large match-sticks, so I can divide the triangle into two pieces of equal size with a single match-stick, using a variety of positions of the stick.
And if it can be done with one, it can be done with any number of match-sticks.
But I think that's not what you're after, and you implicitly assume some rules that you have not explained.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
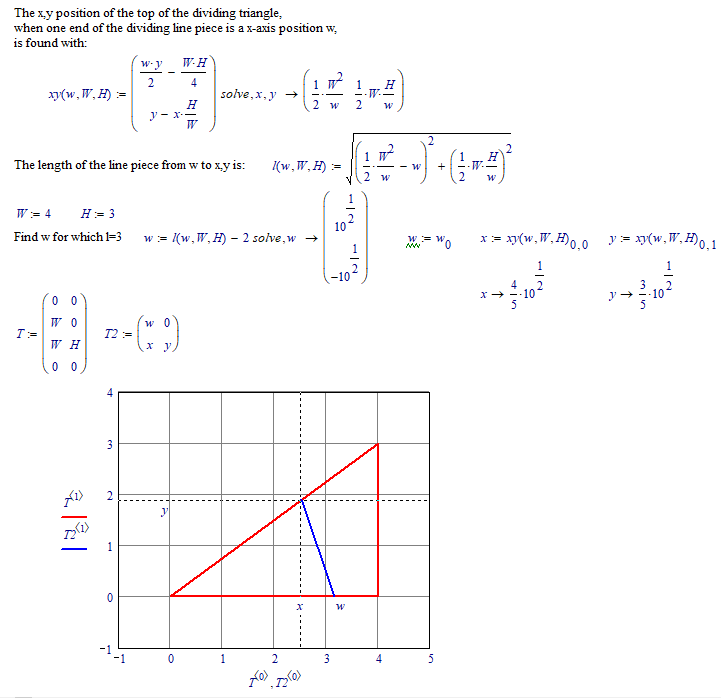
Assuming that only match-sticks with length 1 may be used, and they must be only inside the triangle, here is a solution for 2 match-sticks.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
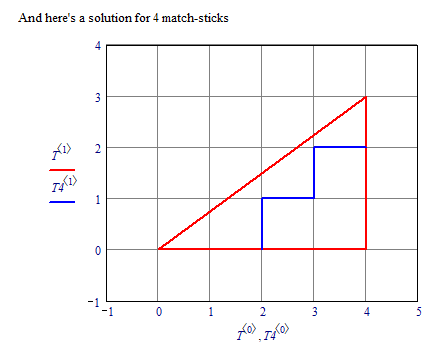
Here's a second solution using two match sticks:
An additional puzzle: Using four matchsticks divide the triangle area in three areas of equal size.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good answers!
Both of you using Mathcad and it will be help for Machcad usage for the users.
Match stick puzzle usually use unit length 1 and it put on dot points on the figure of the stick top or bottom.
Or the position can be fixed by using match sticks.
If you got two and three stick answers, you can arrange them any number of this problem.
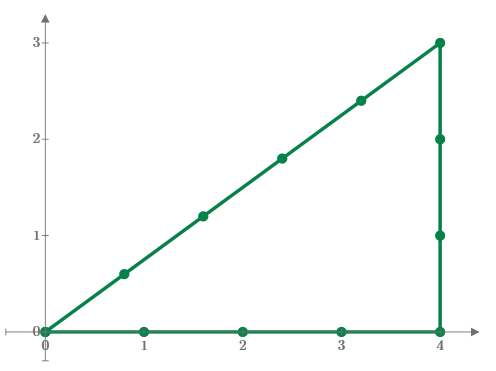
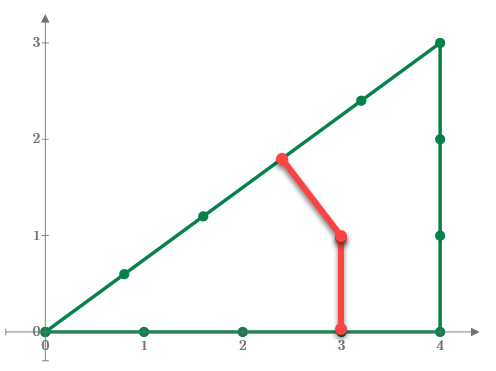
Then, using 12 all sticks in my picture and move two or more sticks to reduce the area size from 4*3/2=6 to 5, 4,3 and 2. I don't know the answer the area size is 1. Of course the minimum movement number of the sticks are the good answers.
Tokoro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
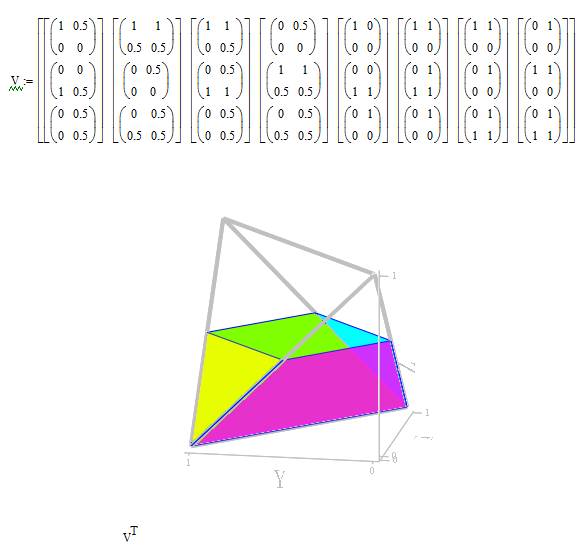
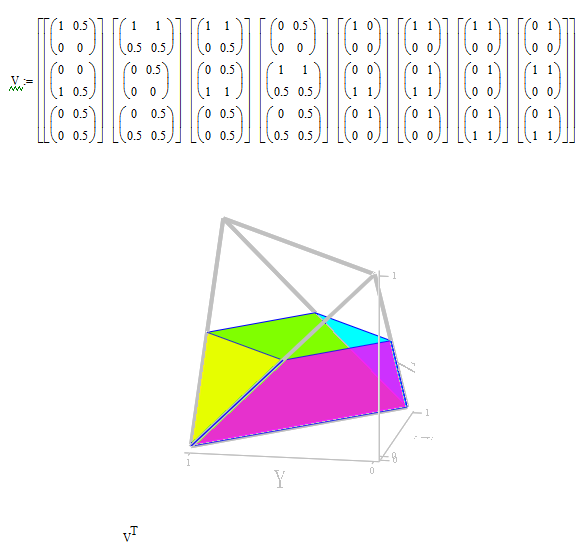
The one of 3D.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
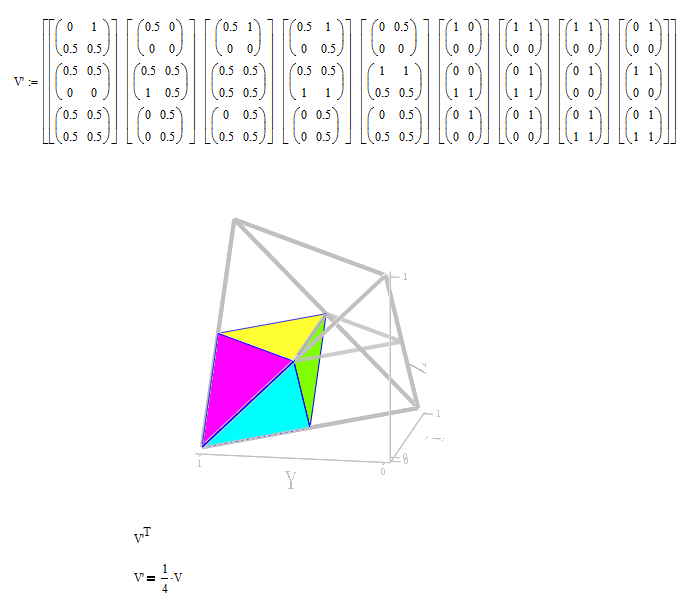
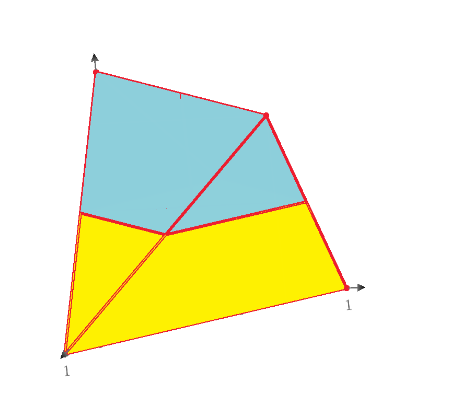
Ttokoro, It seems something like this :
Best Regards.
Loi.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1/4th.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
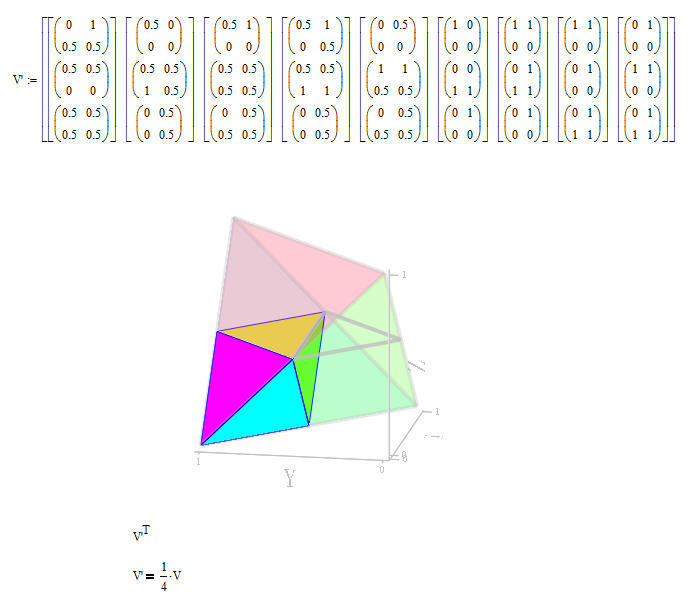
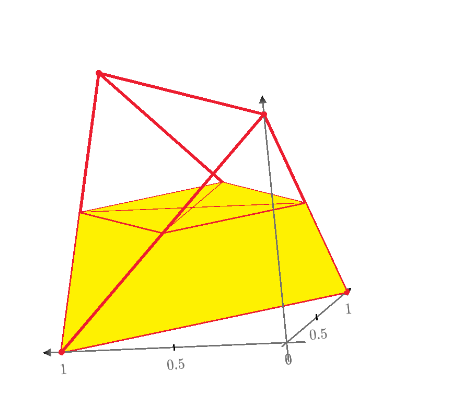
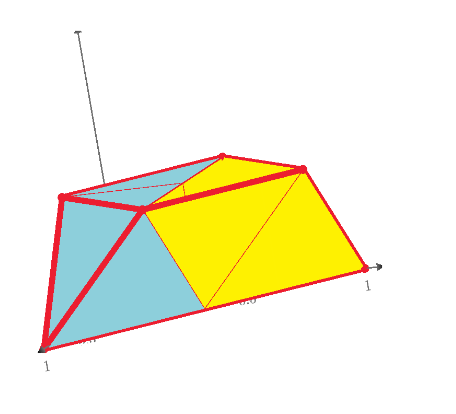
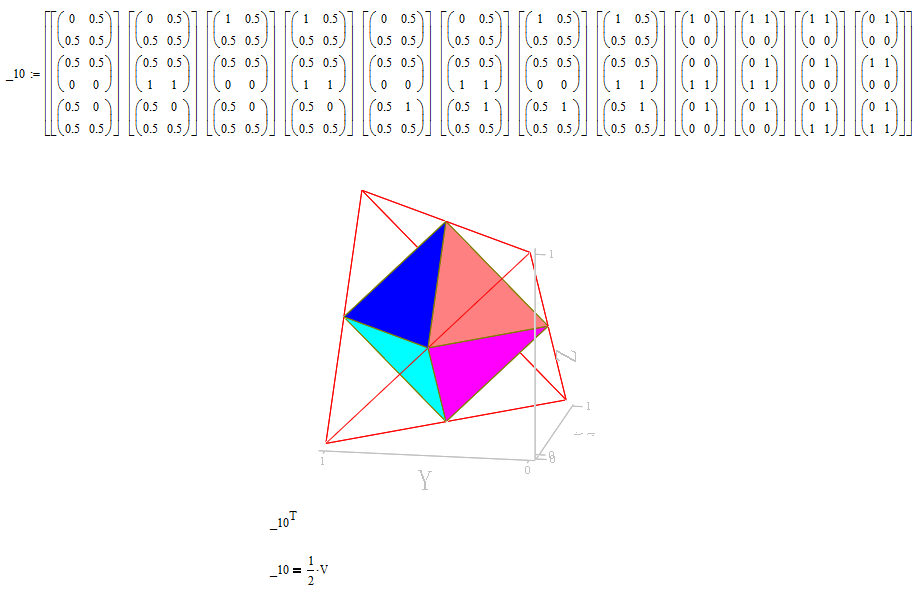
Ttokoro, it seems like this ? :
Regards.
Loi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
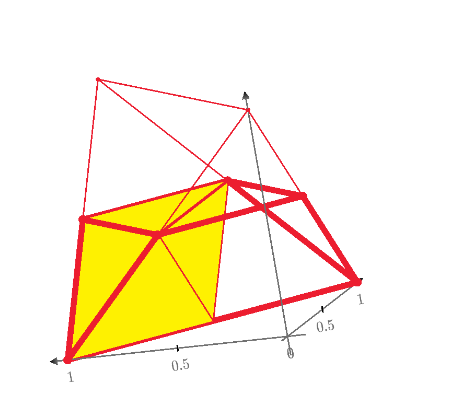
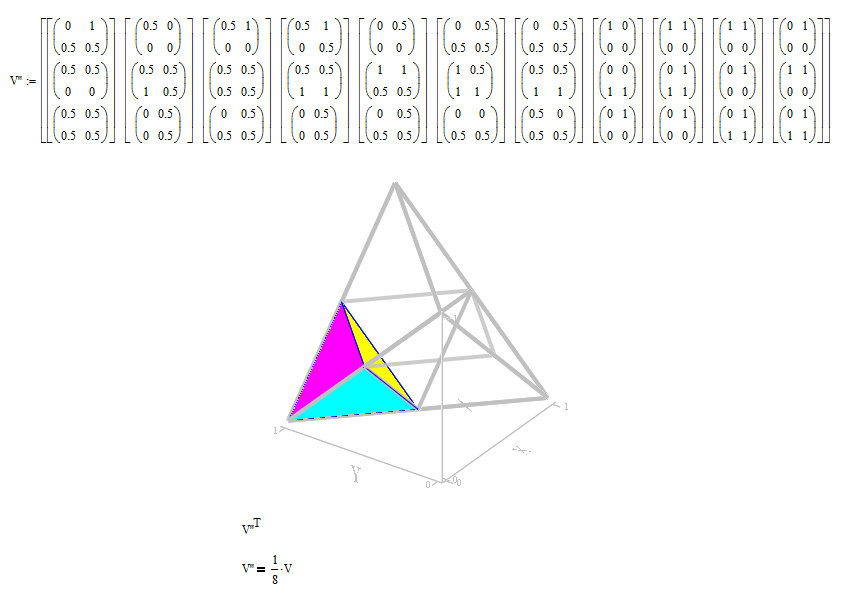
One more third divide by a plane would output a 1/8 V.
Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
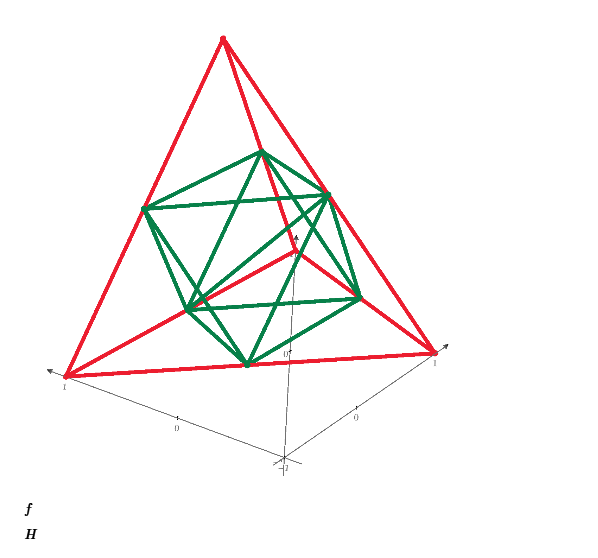
Thanks for your hint, Tokoro. And it seems this is half-volume of "frame".
Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice Job! Oden for kudos.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Prime_6.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
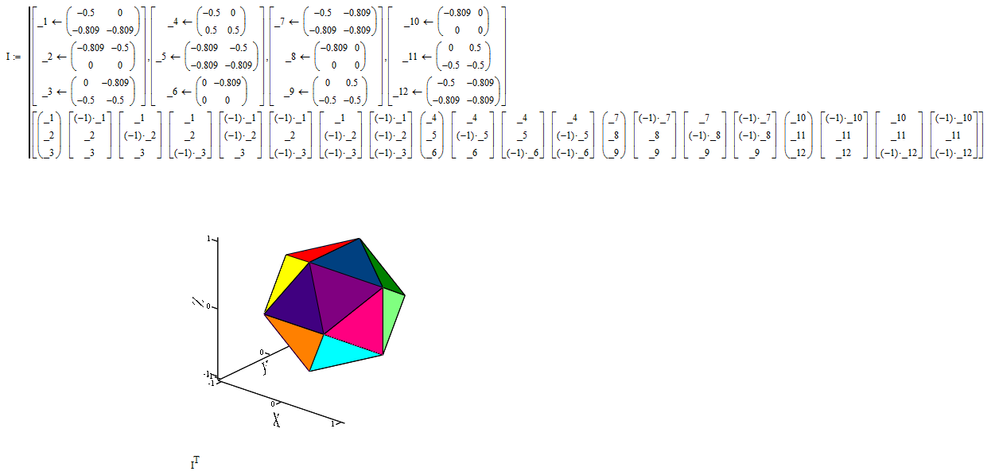
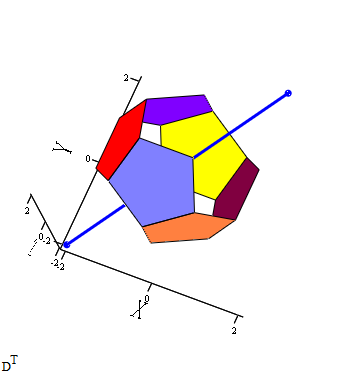
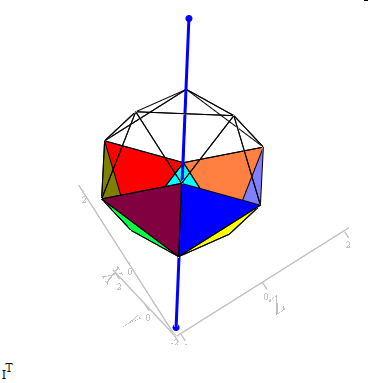
It seems this is last surface patch that I have known about that rotation. (And It seems to divide a surface of regular dodecahedron into equal sized area.)
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Rotation and divide a surface into equal sized areas. (divide by 6 sticks)
Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
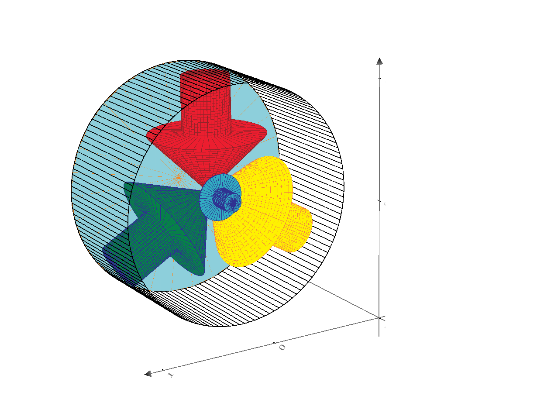
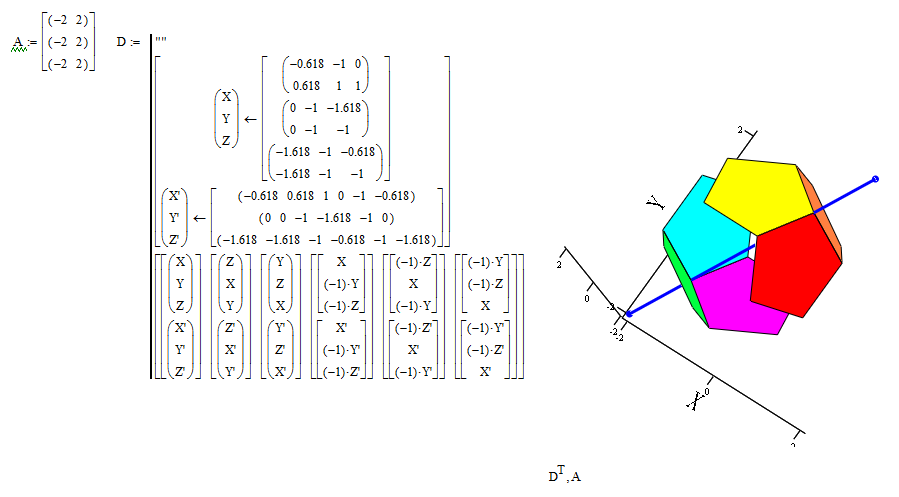
Tokoro, there are two more other planes that divide a surface into equal sized areas :
Best Regards.
Loi.