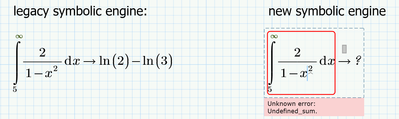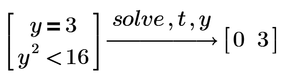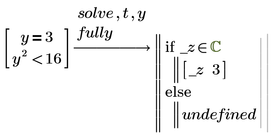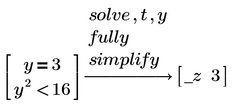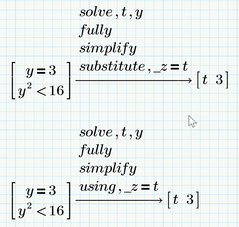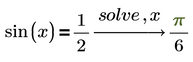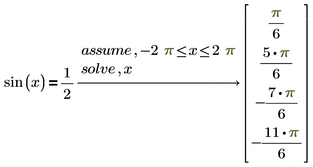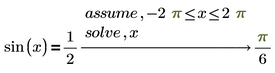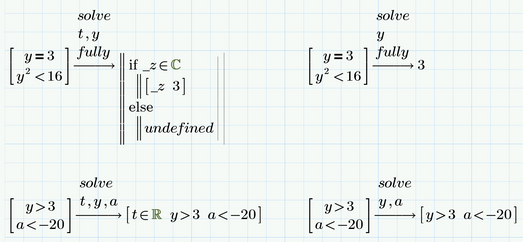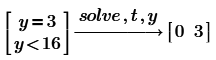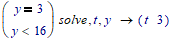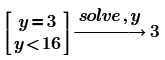Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Dummy Symbolic Solve Variable
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dummy Symbolic Solve Variable
I've seen a couple of PTC articles showing a symbolic solve block using a 'dummy' variable in the solve variable list (which isn't represented in the solve expressions). The examples involved inequalities. They use 't' and it appears needed to force a comprehensive result. I attach a file with two examples.
Does someone know the intention, and interpretation, of this dummy variable?
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What those examples show is that the legacy symbolic engine (muPad, last Prime version it was included with was Prime 6) most of the times refused to solve for a variable which does not appear at all in the given equation or inequalities, while the new (but still less capable) engine gives a more or less meaningful result. Actually a variable not being present in any of the given equations or constraints can take any value you like - it does not make much sense solving for it IMHO.
Fig. 37 shows that in this case the legacy engine returns a wrong result (its also inconsequent that is returns here a result because of the unused variable t solved for), while the new engine returns a correct result.
No software is perfect and there can be found many examples here in the forum where the new engine would return a wrong result whereas the old one gives a correct one. I just found a problem in the new engine
but I am using Prime 6 and it may be that this bug in the new symbolic engine is already fixed in Prime 8.
but back to "solve" and the dummy variable t. I could not see a single example for its use where it would be needed for something useful ( actually I don't consider solving for a non-existing variable to be useful).
Fig.36 shown an inconsistency in the new engine, The doc says (and many example prove it true) that the new engine assumes unknowns to be real numbers unless otherwise stated. consequently in Fig. 38 it returns t element of R. So why in Fig. 36 it says _z in C ? This is a result I would expect from the old engine as this engine assumes all variables being complex unless otherwise stated.
@LucMeekes wondered why Prime suggests t=0 in this example
but this is a well known behaviour also present in older Mathcad version, that the symbolic would just return one single solution in some cases where an infinite number of solutions exists.And for a single solution t=0 might be as good as any.
Often the symbolic can be talked to give all solutions by using the "fully" modifier
and it sure is not wrong to add a "simplify"
To see "t" instead of the generic "_z" you can use the "substitute" or "using" modifier
Talking about differences between the new symbolic engine and the legacy one. Here some examples you won't find in the comparison pages by PTC 😉
You would also get just one single solution if you ask for sin(x)=1/2 to be solved
and adding "fully" gives you all of them
Here the simple and clear result of the old legacy engine
and here what we get from the new engine
it either ignores the assume modifier
or it presents us with a, lets say very unclear expression if we again add "fully" (and "simplify" does not really help)
Examples were done with the new engine in Prime 6. I don't know but its sure possible that PTC has improved it in Prime 8.
To get back to your question and the meaning of that dummy variable t.
As I see it it has no mature effect when using with the new engine and I see no reason why you should use it.
The examples in the help pages simply show that the legacy engine sometimes refused to solve an equation if that unnecessary and nowhere existing variable was in the list of variables to solve for.
IMHO just a very lame attempt to "prove" that the new engine is doing much better.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure why you think that this variable would be needed for anything good??
Can you provide any example where the usage of that kind of extra variable would be vital and necessary?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sure, I was wondering myself. PTC's articles had several examples employing this 'gimmick'. The name you give the variable doesn't appear to matter.
I tried their examples with, and without, the dummy variable, just as you have, above. It seems to force the exposure of a range of, perhaps complex, values which can satisfy the inequalities. I've never seen it documented or explained, so still wondering.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't know whích PTC articles and examples you are talking about.
As you saw its makes no difference in the examples you provided if you omit the variable t in the solve command.
Have you seen and tried any examples where omitting t would make a difference? If so, you may provide them here or at least link to them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A few examples are shown in: https://support.ptc.com/help/mathcad/r8.0/en/#page/PTC_Mathcad_Help/differences_between_legacy_and_new_engines.html# which is a link you helpfully provided to me recently.
Have a look at Figure 33 and a few thereafter.
I can't say I fully appreciate the significance of this, but PTC included this dummy variable with some intentionality, so I thought I'd inquire. It seem to force expression of a domain and range of the results obtainable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fig 33 shows the result of the legacy symbolic, it can't solve.
Fig 34 shows the corresponding result of the new symbolic. it solves,
but i wonder why t should be 0, I guess it would be more appropriate to have t be an element of R, as in Fig 38. Though I must say that the answer provided by Mathcad 11 (with Maple being the engine) is still better:
Note that you don't need the t, it solves y simply with:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What those examples show is that the legacy symbolic engine (muPad, last Prime version it was included with was Prime 6) most of the times refused to solve for a variable which does not appear at all in the given equation or inequalities, while the new (but still less capable) engine gives a more or less meaningful result. Actually a variable not being present in any of the given equations or constraints can take any value you like - it does not make much sense solving for it IMHO.
Fig. 37 shows that in this case the legacy engine returns a wrong result (its also inconsequent that is returns here a result because of the unused variable t solved for), while the new engine returns a correct result.
No software is perfect and there can be found many examples here in the forum where the new engine would return a wrong result whereas the old one gives a correct one. I just found a problem in the new engine
but I am using Prime 6 and it may be that this bug in the new symbolic engine is already fixed in Prime 8.
but back to "solve" and the dummy variable t. I could not see a single example for its use where it would be needed for something useful ( actually I don't consider solving for a non-existing variable to be useful).
Fig.36 shown an inconsistency in the new engine, The doc says (and many example prove it true) that the new engine assumes unknowns to be real numbers unless otherwise stated. consequently in Fig. 38 it returns t element of R. So why in Fig. 36 it says _z in C ? This is a result I would expect from the old engine as this engine assumes all variables being complex unless otherwise stated.
@LucMeekes wondered why Prime suggests t=0 in this example
but this is a well known behaviour also present in older Mathcad version, that the symbolic would just return one single solution in some cases where an infinite number of solutions exists.And for a single solution t=0 might be as good as any.
Often the symbolic can be talked to give all solutions by using the "fully" modifier
and it sure is not wrong to add a "simplify"
To see "t" instead of the generic "_z" you can use the "substitute" or "using" modifier
Talking about differences between the new symbolic engine and the legacy one. Here some examples you won't find in the comparison pages by PTC 😉
You would also get just one single solution if you ask for sin(x)=1/2 to be solved
and adding "fully" gives you all of them
Here the simple and clear result of the old legacy engine
and here what we get from the new engine
it either ignores the assume modifier
or it presents us with a, lets say very unclear expression if we again add "fully" (and "simplify" does not really help)
Examples were done with the new engine in Prime 6. I don't know but its sure possible that PTC has improved it in Prime 8.
To get back to your question and the meaning of that dummy variable t.
As I see it it has no mature effect when using with the new engine and I see no reason why you should use it.
The examples in the help pages simply show that the legacy engine sometimes refused to solve an equation if that unnecessary and nowhere existing variable was in the list of variables to solve for.
IMHO just a very lame attempt to "prove" that the new engine is doing much better.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree fully with Werner's and Luc's comments - did so beforehand which is why I brought it up.
And man! That example of sin(x)=1/2 is ugly!