Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
E-Numbers in symbolic result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
E-Numbers in symbolic result
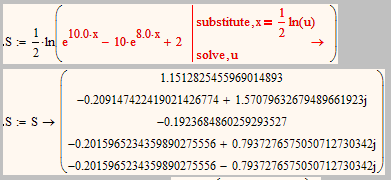
Can anyone explain what the meaning of those changing E-Numbers could be?
They change whenever the sheet/expression is recalculated, so I suppose this to be some internal variables of the symbolics engine which should never show up, right?
Doing a manual sybstitution Mathcads symbolic is able to find the solutions.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
and what is it X:

Try please more - solve, fully!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
I was aware of the effect which we get when using integers. This was the reason the symbolics was forced on purpose to decimals by writing 10.0, etc. The eval of the full integer expression shows that Mathcad is doing the right substitution (and the internal variable X508 makes sense) but somehow is not able to resubstitute the way I have done later in the file. Showing that E-variable does not make sense and should not been done. BTW, the expression ln(E...) in the denominator should be simply 1, then we would get at least the positive solution 1.151.
Its a bug in my opinion, as Mathcad should show all solution - its capable of finding the five roots (for _z) anyway as i have shown in my sheet and is able to take the log of those values. With "fully" I would expect Mathcad to add sort of k*pi to the imaginary parts. I was not expecting Mathcad to solve that fifth degree equation in exact mode.
Valery Ochkov wrote:
and what is it X:
Try please more - solve, fully!
???? Did you try it yourself? It doesn't get rid of those internal variables - on contrary!
Or am I missing your point?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
???? Did you try it yourself?
Yes I did.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
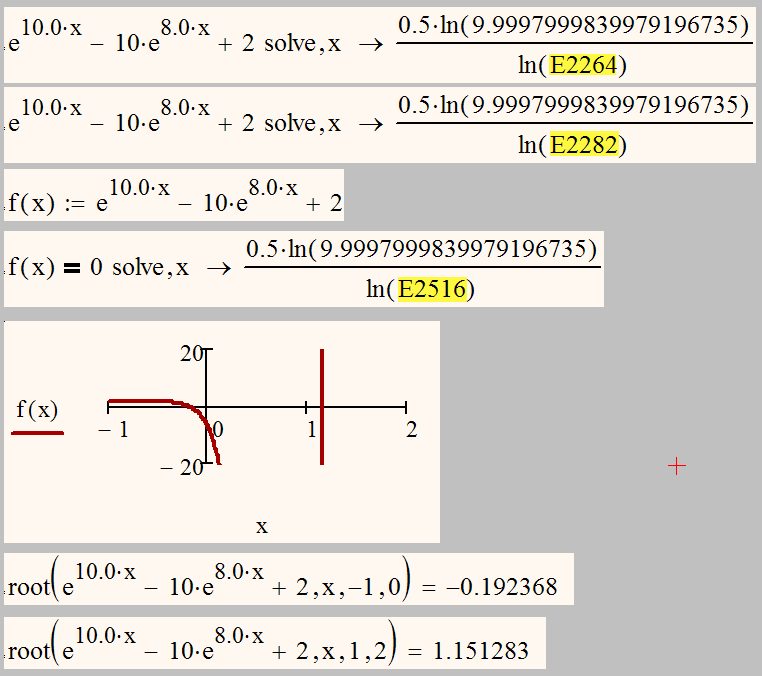
I've no idea why the ln(Exxx) numbers appear, but dividing through by e^(-10x) or e^(-8x) allows the symbolic solver to find numerical solutions (though only one at a time):
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
I've no idea why the ln(Exxx) numbers appear, but dividing through by e^(-10x) or e^(-8x) allows the symbolic solver to find numerical solutions (though only one at a time):
Alan
Funny effect. I stumbled upon this on trying to solve an equation similiar to the second one of yours a different way. The E-numbers should simply be Euler e, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Partially solve this problem - to replace the variable
Viktor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your interest.
I thinks thats basically the substitution I used later in my file (your y being my u)
Mathcad seems to use that substitution internally but for some reason is not able to do the resubstitution correctly.