Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Error in solving equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Error in solving equation
Hello everyone
I need to find the value of a variable (Dev) per iteration, assigning an initial value, but I get error and truth do not know why.

Hope you can help
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
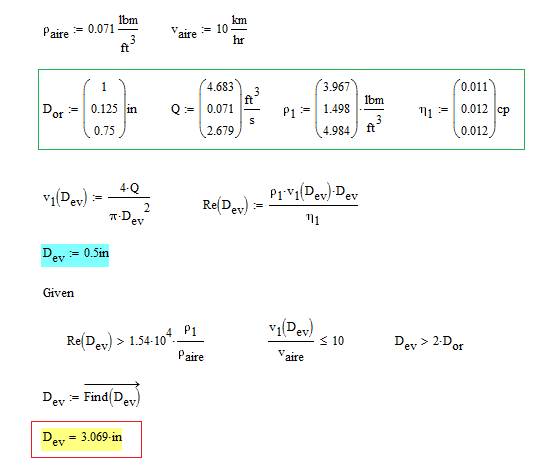
You could do as I already wrote and solve for all three unknowns, but I thought it would be a better idea to turn Re and v.1 into functions of D.ev which they obviously are.
Now there are only three inequalities for D.ev left and not a single equations. So you have a range of valid values for D.ev and Find will give you the smallest one (3.069 in). If you chose different(higher) guess values you get different results.
In your second solve block there is a unit mismatch.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attach your file, not just a picture.
It looks to me that v.1 and Re are unknown, too, and so you will have to search for all three unknowns and provide guesses for all of them. But you only have two equations!??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You could do as I already wrote and solve for all three unknowns, but I thought it would be a better idea to turn Re and v.1 into functions of D.ev which they obviously are.
Now there are only three inequalities for D.ev left and not a single equations. So you have a range of valid values for D.ev and Find will give you the smallest one (3.069 in). If you chose different(higher) guess values you get different results.
In your second solve block there is a unit mismatch.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner. One last question, as I can do to calculate "Dev" for each value in the case of multiple input values.
Thanks in advance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It may work if you vectorize ALL calculations dealing with those vectors.
The other (and in my opinion better) way is to make v1, Re functions of Q, p1, etc and turn the solve block into a function of all those variables you like to change. Then call that function with your vectors as arguments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vectorized functions not work, but the second way, worked perfectly.
Again, many thanks werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bryan Pérez Pérez wrote:
Vectorized functions not work, but the second way, worked perfectly.
Again, many thanks werner
Both ways work and you don't even need to vectorize for the first approach. You only have to set up the guess as a vector.

------------------------------------------------------------------------------------------------

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
You only have to set up the guess as a vector.
I didn't know you could do that ![]()
As for the results. It possible calculate the minimum and maximum values (Dev_min and Dev_max) satisfying these three equations?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As for the results. It possible calculate the minimum and maximum values (Dev_min and Dev_max) satisfying these three equations?
Not with Find(). It seems you get the lowest value if you provide a very small guess, but if you provide a very high guess value, you don't get the upper limit of your range - at least not reliably.
You can use a dummy function f(x):=x and use Minimize(f,D.ev) instead of find to get the minimum valeu. But for reasons unknown to me maximize() failed.
You can add D.ev<0 as constraint and end the solve block with minerr(D.ev) to get the minimium. If you change the constraint to D.ev > 100 in you should get the maximum value.
But I guess because your inequalities are simple enough the most obvious way to deal with the whole problem is to directly solve the inequalities to get the range of allowed values for D.ev:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello everyone
Like the startup problem, trying to solve an equation me an error occurs, I hope you can help me.
Attached worksheet with the problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Right click on the error and chose "Trace Error" and then "First" to get more information why the solve block failed.

In your case you typed "e^S" instead of "e^S(P.1)".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I did not know the tool you used (Trace error), thank you very much Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Error messages, especialy in solve blocks leave a lot to be desired. The only error message a solve block ever will throw is the "unknown variable" message, no matter what the real cause may be. Using "trace error" often (but not always) can help to track down the real reason for the solve block failing.





