- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Error propagation - How can help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Error propagation - How can help?
Dear Friends,
I know, I might know it, but I would like to ask.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Variance(a*X)=a^2*Variance(X)
When you calculate the inverse the variance cannot be calculated exactly, but it's approximately Variance(1/X)=Variance(X)/mean(X)^4. The approximation is good as long as the mean is many standard deviations away from 0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard, thanks. SOrry But I do not mean the Variance but the STANDARD ERROR SE, which is given and wanted.
Moreover I have found this: Could this be also the right answer, I am little confused to compare these two.
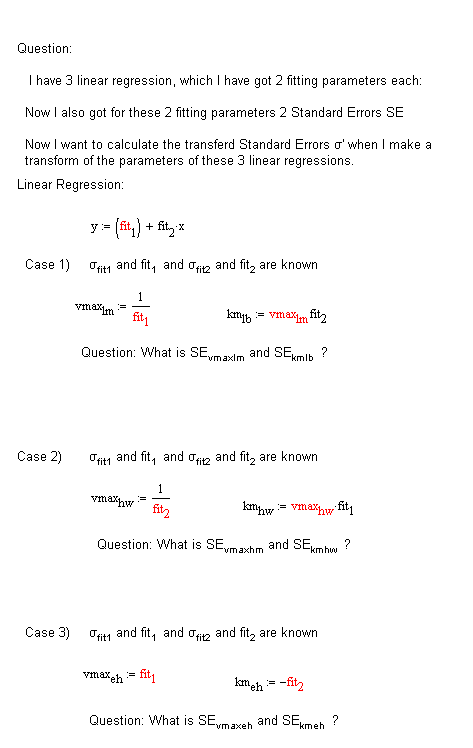


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The variance is the square of the standard deviation. The standard errors are standard deviations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok, Thanks a lot. ANd what is the Variance from Variance(fit1)/Variance(fit2) ?
I get: VAR(fit1)/mean(fit2)^2 + mean(fit1)^2 * VAR(fit2)
Is that correct?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If x and y are independent,
Var(x*y)=Var(x)*Var(y)+Mean(x)^2*Var(y)+Mean(y)^2*Var(x)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard, is that ok?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That looks right ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Walter. In your material you have some mixing things.
Formulas from point 2.1 (in german) are for calculate the "propagation of erros". For example, if the surface is S = x*y then dS/dx=y, dS/dy=x then (D = delta, d=partial d) DS = sqrt( (dS/dx*Dx)^2 + (dS/dy*Dx)^2) ) = sqrt( (y*Dx)^2 + (x*Dy)^2 ). That's cool but useless. In the practice what is taken for propagating errors is DY = Sum(abs(dY/dx[i])*Dx[i]). Applied this other to DS = y*Dx + x*Dy, then DS/S = Dx/x + Dy/y: this is the error for the area is the sum for the errors of the factors. Notice that this formula is coherent with the usual form where errors are taken: as abs(Y2-Y2), this is difference only in the vertical axis, not as (more correct, but impractical) the distance between two points, which is sqrt(Dy^2-Dx^2).
So, even your formula in the book is correct, is ... is ... german. Is exact but not which is used in the practice.
The manipulation of the varience that you are using isn't related with this other formulation, and came only from the definition of the Varience by itself, as Var(X) = E[(X - E[X])^2]. For that, the general result is that Var(f(X)) = (aprox) f ' (E[X]) ^2 * Var(X), provide some regularity conditions (f '' continous and E[X] and Var[X] finites). That´s a Taylor approximation.
This is not the case for 1/Y, so can´t use it "as is". Use the second moment based in more accurate Taylor polynomial (the next). So, I guess that your formula is here: Taylor expansions for the moments of functions of random variables - Wikipedia, the free encyclopedia (the last one, with Covar including)
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I got the formula for the variance of 1/X from here: http://stats.stackexchange.com/questions/41896/varx-is-known-how-to-calculate-var1-x
It is based on the Taylor expansion, with just the first term being retained. Apparently that's OK as long as the mean is many standard deviations away from 0. The other formulas are exact (although the one for Var(x,y) is only correct if x and y are independent. If they are not, there are other terms that include the covariance).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard, yes, you're right. With first derivative give enough approximation (first I guess not, because 1/X is hard to approximate with only one derivative), as is showed in your reference, and Covarience is only for non-independent variables. 2 - 0!
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
first I guess not, because 1/X is hard to approximate with only one derivative
This was a surprise to me too. The approximation is not good close (in units of standard deviation) to zero though, so it is only useful to Walter if the variable in question is a not close to zero. Based on other threads, I believe that in this case that is true, but this approximation certainly cannot be taken as a universal answer to the question of "what is the variance of 1/X when the variance of X is known".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Richard for cover my mistake in that way, you're a gentleman. Point is that you don't stop in your original guess and research for validate or discard it, me don't.
Anyway, for me is suspicious the documentation that Walter attach, about error propagation. Just because is the opposite for static methods, this is, as can read, you start from Y=Y(X1,...Xn), this is the exact formula for Y, and then derive the error from this formula by the gradient and individual errors Xi, while Ymean is evaluated with Xmean, etc. If you use fit: what are fitting? Parameters in Y? Then you know the Y exact form (not formula, which is with parameters evaluated) but fitting get the parameters, and want the error in the parameters? Is it that the procedure showed?
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Alvaro.
My originate problem to get the STANDARD ERRORS for v and k in
Case 2)
It`s the Hanes-Woolf fomulea https://en.wikipedia.org/wiki/Hanes%E2%80%93Woolf_plot
from the linear regression of the obtained points I get 1/v and k. The y-axe is S/v where S is a constant. When I want to calculate now v I just calculate 1/fit2. Morerless I want to get the SE fit1/fit2.
That is clear. But I also get an Standard Error from the regress for 1/v. Now I would like to get the STANDARD ERROR for v from this calculation.
I hope I could explain what I am looking for.
Case 1) is the Lineweaver Burk equ. https://en.wikipedia.org/wiki/Lineweaver%E2%80%93Burk_plot
there I want to get the SE for 1/fit1 and fit2/fit1.
Case 3) is the E.-Hofstee equ. http://what-when-how.com/molecular-biology/eadie-hofstee-plot-molecular-biology/
Here I want to get SE(V) = SE(fit1) and SE(k) = SE ( -fit2 ).
It would be fine if I could get correct formuleas for the 3 Cases to get the correct SEs for the 2 Parameters.
I hope I could clearify what I am looking for. Moreover I have attached a paper where these 3 cases are compared.
Thanks a lot
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alvaro, thank you for your statement.
I found that:
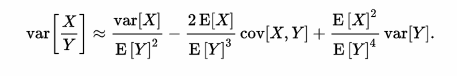
So is E[X] = mean[X] and E[Y]=mean(Y). If I have only the parameters X +- DeltaX and Y +- DeltaY then mean[X]= X and mean[Y]=Y.
Could this be correct ? And what is cov[X,Y] when I have only the obtained fitting parameters fit1 and fit2? I do not have a distribution! I have only 2 numbers!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks Alvaro, in your reference https://en.wikipedia.org/wiki/Propagation_of_uncertainty was:
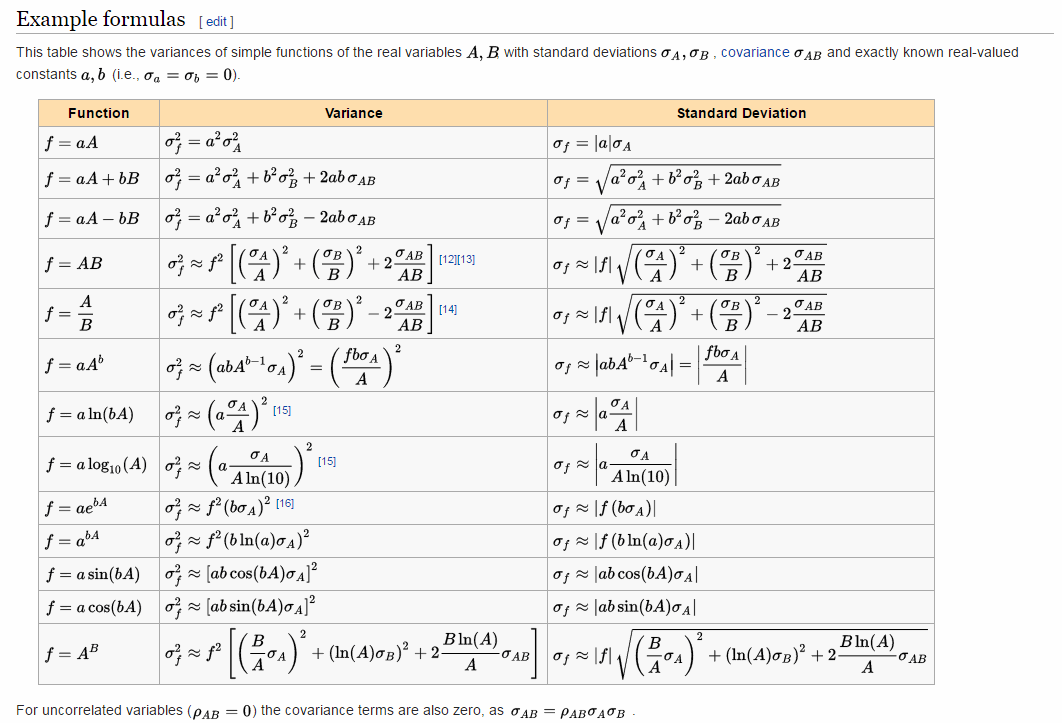
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your formula is another Taylor expansion. If x and y are not independent then
Var(x*y)=Var(x)*Var(y)+Mean(x)^2*Var(y)+Mean(y)^2*Var(x)+Cov(x,y)^2+2*Mean(x)*Mean(y)*Cov(x,y)
where Cov(x,y) is the Covariance of x and y. This formula is exact.
And what is cov[X,Y] when I have only the obtained fitting parameters fit1 and fit2? I do not have a distribution! I have only 2 numbers!
Assuming your model is correct, there are two numbers, call them x and y, that describe the data. What you have from the fit are only estimates of those two numbers, because your data has errors. If you have a second set of data you will get a different estimate. All the possible estimates for each number form a distribution, with a mean and a standard deviation. The numbers you get from the fit are estimates of the means of the distributions, and the standard errors are estimates of the standard deviations of the distributions.
When you calculated the standard errors by hand, at one point you generated the variance-covariance matrix. The diagonal elements are estimates of the variances, and the off-diagonal elements are estimates of the covariances. If x and y are independent then the estimates of the covarianecs should be small.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Richard, you open my eyes with your great and easy explanation. That I have understood. But please understand the basic of my problem. I have a linear regression when I substitute y by 1/S. I get an for the regression y=kx+d two parameter k and d with an Standard Error. Now I want to get the Standard Error for S by re-transforming s = 1/y. When I calculate the COV(X,Y) of my dataset X and Y I get a neg factor under the SQRT. I am a little bit confused. ![]()
The reason for making the y axe as 1/S is that I can get so a linear dependence for my X and Y, wich can be solved by my linear regression.
I hope I could explain it correct.
Did you understand, what I mean to explain?
I have added a example MathCAD Sheet for Case 2) Hanes-Woolf. (See at the end the QUESTION)

Thanks
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have a linear regression when I substitute y by 1/S. I get an for the regression y=kx+d two parameter k and d with an Standard Error. Now I want to get the Standard Error for S by re-transforming s = 1/y. When I calculate the COV(X,Y) of my dataset X and Y I get a neg factor under the SQRT. I am a little bit confused.
The reason for making the y axe as 1/S is that I can get so a linear dependence for my X and Y, wich can be solved by my linear regression.
You fit s=k*x+b, to get two coefficients k and b, with standard errors. If s=1/y then y=1/(k*x+b). The coefficients have not been transformed, so the standard errors do not need to be transformed.
I don't understand what you mean when you say "When I calculate the COV(X,Y) of my dataset X and Y I get a neg factor under the SQRT".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi. What Richard say is very correct. Fitted coefss remains untransformed, so, they precision is the precision from the definition.
From your reference is the attached picture. Is the same process that I explain in the previous post, but taking Delta Y = Sum (abs(dY/dx[i]), which is more simple, given the usual error propagation formulation for area, and the more precise definition, using Pithagoras, is more complicated. That kind of complications introduce in practical calculus errors, human ones, and not derived from the theory (even human realibity is fashion right now, and a new object under study). Precisely, for this I love Mathcad: units, dynamic calculus (like excel) and explicit formulas showing (unlike excel) reduces my human uncertain.
This complicated procedure intruduce the minus sign, and, it's just an approximation, so, don´t surprise if the radicand results negative. I guess that you can take the abs value for the entire radical, and return it into the reals.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi. Again. Actually, from the wiki article references, can't found my derivation in: http://web.mit.edu/fluids-modules/www/exper_techniques/2.Propagation_of_Uncertaint.pdf
I prefer that other formulation, more simple. At least, all are aproximations.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes Alvaro, I think you are on the same way as me. IT might be the Sum((dy/dx(i))^2). As the cov(k,b) = 0 then it agree again to your statement and to my originate Error Propagation copy in German. Moreover your reference from the MIT do a great explanation of this Gauß'sche Error Propagation Law.
I think for my approximation I will do the Sum((dy/dx(i))^2).
Thanks
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
An if I do that: Then I get:
but before we got form wiki: dq = SE(fit1)/fit1^4 !! Why?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Because came from two different worlds. That was my first observation: you're using two very different models. One from calculus of probabilities, which is a theory of the measure, established as a sigma - algebra (that's complex!), and the other from traditional infinitesimal calculus, using the Taylor approximate for one or multiple variables, which simply replace the real curve or surface by a rect or a plan given by the derivative or the gradient. Where distances are measured with Pitagoras, or with more simple abs(y2-y1)
Remember that the other usual theory of measure came or from reals directly as axioms, or form naturals (cardinals, not ordinals) from Peano's axioms. Actually ordinals are more related with probabilities.
Even different, both are correct, as both are approximations from the "true" error.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Richard, I am not wure if I had explained it correctly or you have misunderstood me. But the SE must transformed too. I think so.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why do you think the standard errors need to be transformed? You say "I get an for the regression y=kx+d two parameter k and d with an Standard Error. Now I want to get the Standard Error for S by re-transforming s = 1/y.", but k and d are coefficients, and S is the dependent variable. S=1/(kx+d), so the standard errors in k and d are what they are; the coefficients have not been transformed in any way. Certainly, the confidence limits for S are not the same as the confidence limits for y, but there is no transformation of the standard errors needed to calculate them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
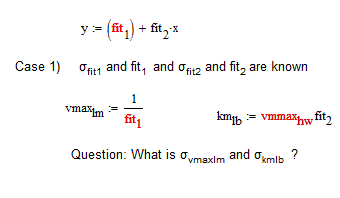
for fit2=0 I get vmax = 1/fit1. and when I get for fit1 a standard Error I also get a Standard Error for vmax but this might be not the same as for fit1. Imagine, you have and dfit1 = 0.1 then for v it can be the same! Accoring the Gauss Error Propagation Law, (see the Link from MIT http://web.mit.edu/fluids-modules/www/exper_techniques/2.Propagation_of_Uncertaint.pdf ) there is a mathematical further processing of fit1. the Function is 1/y. As there is only one variable in the further processing function the relative error is the same. But the absolute error..
For km=vmax*fit2 = fit2/fit1. Here I have 2 variables in the further processing function. So the relative error for km is accoring
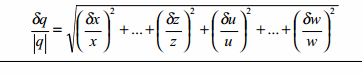
the ( SQRT (dfit2/fit2) ^2 + (dfit1/fit1)^2 ) .. The Pythagoras as Alvaro said. Tha Absolut error is the relative error * fit2/fit1.
I hope I could make it more clear.
Moreover I found this paper online: http://pubs.acs.org/doi/abs/10.1021/ed1004307
Here from this paper:

Best regards
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just find, if the slope and intercept is not independent than there must be calculated the covariance !
http://pubs.acs.org/doi/pdf/10.1021/ed074p1339
(here I have attached the Note)






