Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Exponential Fit Curve Help
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Exponential Fit Curve Help
Hello,
I am trying to create a best-fit curve for a data set. I have imported two excelsheets containg the data into Mathcad. Each excel contains 1066 intergers. I have plotted them using the x-yplot functionality. The plot appears to follow an exponential projection. So, I tried to obtain exponential fit curve using the expfit() function. However, the fit function that I obtained is not correct, because it does not fit the data.
Please advise what I shoulddo to obtain the proper exponential fit curve.
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please post a worksheet with the data. We can show you how to perform a generalized fit that can be applied to any function (but I don't know what that function might be without seeing the data).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Could you show me how to plot an expfit() function first . I am trying to plot it in MathCAD.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, but I can't plot an expfit function if I don't have data to fit it to ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please see in attachment (this worksheet is taken from "Mathcad Help").
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have you read the Mathcad Help files on using that function and curve fitting in general?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Jan Kowalski,
Thanks for sending me your sample mathcad files. They have been very helpful.
Now, I am trying to come up with a correlation coefficient associated with the curve fits. I tried using the function corr(A,B), as explained in the Mathcad Help site. However, I am not sure if I am using this fucntion correctly. How do I link the corr function with the fit curve? Are the varibable A, B supposed to be the raw data, or should I use the data from the curve fit? Please explain.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It would be time you begin attaching worksheets, don't you think so, too?
Are the varibable A, B supposed to be the raw data, or should I use the data from the curve fit?
Both! As you want to compare the original data (Y) to the fit data you get by the derived function H, you have to throw both into the corr function. First you have to create an apprpriate vector of fit values.
In lack of a sheet from yours I have taken one of the sheet Jan has provided to demonstrate.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please be aware however that the correlation is no measure of a good fit. You will get exactly the same correlation value if you multiply Y by any constant.
A measure of fit would be the sum of square of difference between Y and fitData
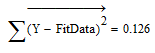
0 would mean a perfect fit (identity).
Better use the mean squared error as it takes in account the number of points. This would be the above divided by the number of points (length(Y))





