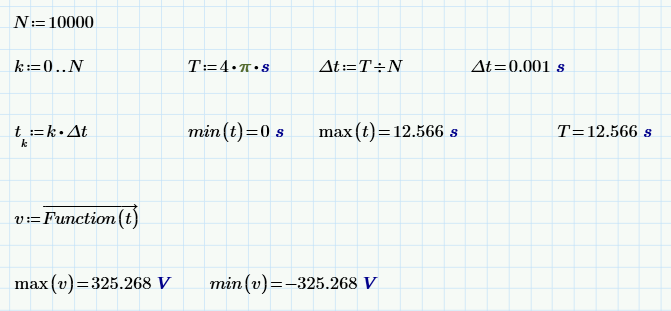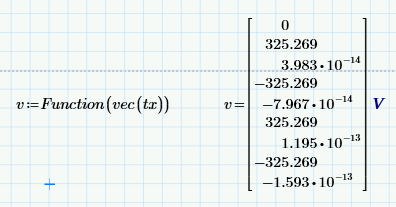Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Find minima and maxima of a function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find minima and maxima of a function
Hello all,
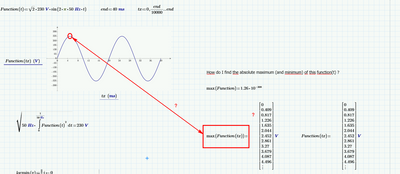
as a simple example I use a sinus function where I want to find the absolute minimum and absolute maximum.
If the function will be more complicated then the local extrema are not interesting currently. I am looking for the absolute values.
To be honest I don´t want to make a derivation d/dt and find the corresponding times via solve block.
I would like to use some kind of integrated function.
Unfortunately "max(vector)" and "min(vector)" does not work. My function f(txx) seems to be not an array ... Hm.
Also I have found in the F1 help menu a function for local minima and local maxima. I understand that it compares the array elements but it also doesnt help.
Can you help please? My sheet is attached. Also here the screenshot:
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are several approaches to solving this problem - here's one.
Note that k is a range variable - which is most assuredly not a vector. k is chosen to be an integer range variable so that it can be used as a vector index. t is a vector. The vectorized operator is used to ensure that Function is applied to each element of t, and the result is assigned to variable v.
max and min then return the values you are looking for - unless a Jedi Mind Trick has meant that the values of t don't exactly coincide with the true values that give the max & min of Function. The choice of interval below should give near enough the true min & max:
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are several approaches to solving this problem - here's one.
Note that k is a range variable - which is most assuredly not a vector. k is chosen to be an integer range variable so that it can be used as a vector index. t is a vector. The vectorized operator is used to ensure that Function is applied to each element of t, and the result is assigned to variable v.
max and min then return the values you are looking for - unless a Jedi Mind Trick has meant that the values of t don't exactly coincide with the true values that give the max & min of Function. The choice of interval below should give near enough the true min & max:
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes!
My time was not a vector, it was a range variable. With your trick it´s all fine 🙂
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No worries.
There are other ways of dealing with range variables. Here are a few program versions:
I find the function vec to be quite useful in many circumstances (although I tend to use a slightly more complicated, recursive version that completely flattens even deeply nested arrays).
Here's vec being used to directly convert the range variable tx as Function's argument.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using the derivative might seem like the most accurate way to solve the task but you may run in multiple problems. With simpler function you may be able to use the symbolics to find all extremas in a given range and then chose the absolute ones. But with just slightly more complex functions the symbolics might be overwhelmed. And when you switch to numeric evaluation via "root" or a solve block, you get only one solution (depending on a guess) which is not much helpful.
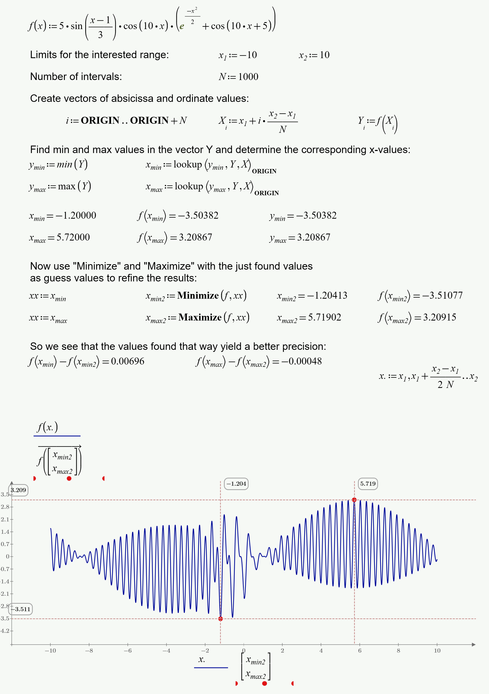
So using the brute force way by creating a vector of equidistant x-values and calculating the corresponding y-values and then use "min" and "max" seems to be the most appropriate. A disadvantage might be that too few values in the vector will give an inaccurate result (especially for high frequencies and an larger range) while creating a very large vector might eat up too much resources (time, memory, ...).
One possible approach could be to follow the step with "minimize" and "maximize" (these functions usually only find local extremas) with the just found values as guess values.
The following example shows what i am talking about:
Prime6 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Helpful solution @Werner_E . I just used this hybrid approach for finding global max. values and it worked great!