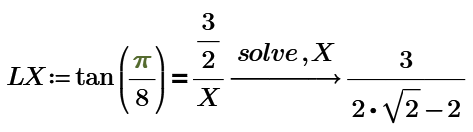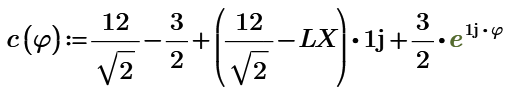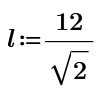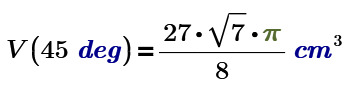Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
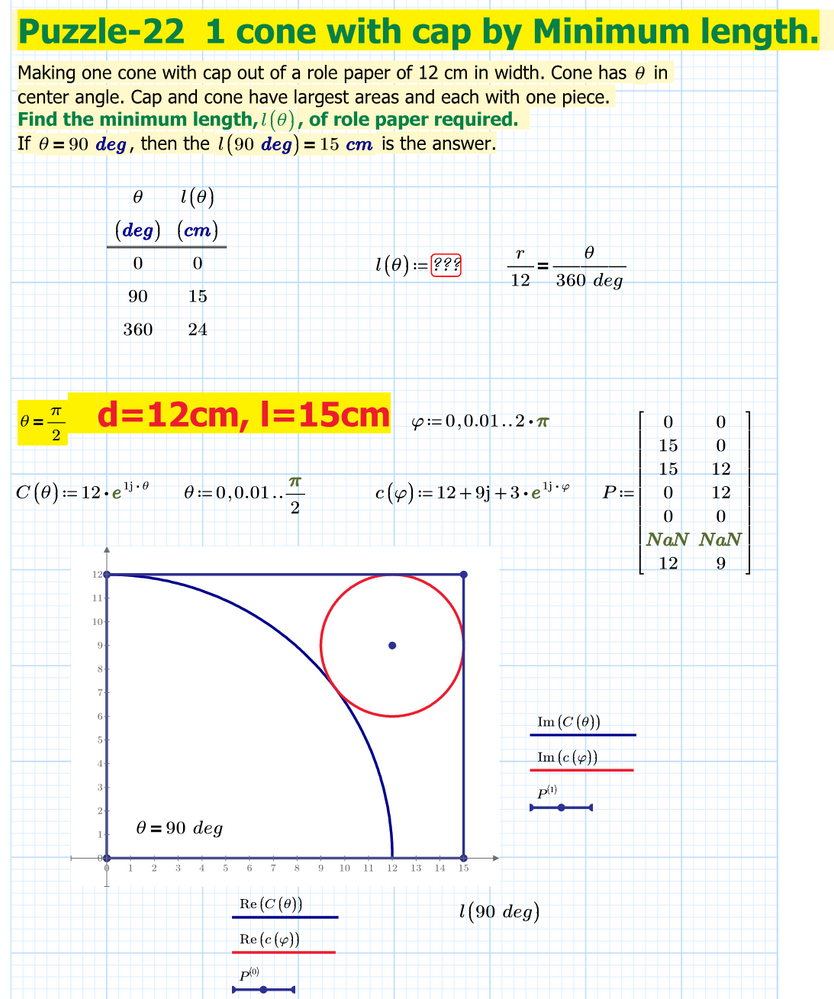
Find the minimum length, l, of role paper required.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find the minimum length, l, of role paper required.
Making one cone with cap out of a role paper of 12 cm in width. Cone has θ in center angle. Cap and cone have largest areas and each with one piece.
Find the minimum length, l(θ), of role paper required.
If θ=90deg, then l=15 cm is the answer.
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
-
Puzzles Games
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I understand what you do. I just think its inconsistent to forbid making the cone larger than 12 cm side length (like in Lucs 45° solution) but accept to make it smaller for angles larger than 180°. Just my 2 cent.
I would rather stay with "largest surface but minimal paper" throughout or with constant side length 12 cm and minimal paper (which would allow only angles from 0 to pi.
Here a numerically derived solution for the latter:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can add to the table:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
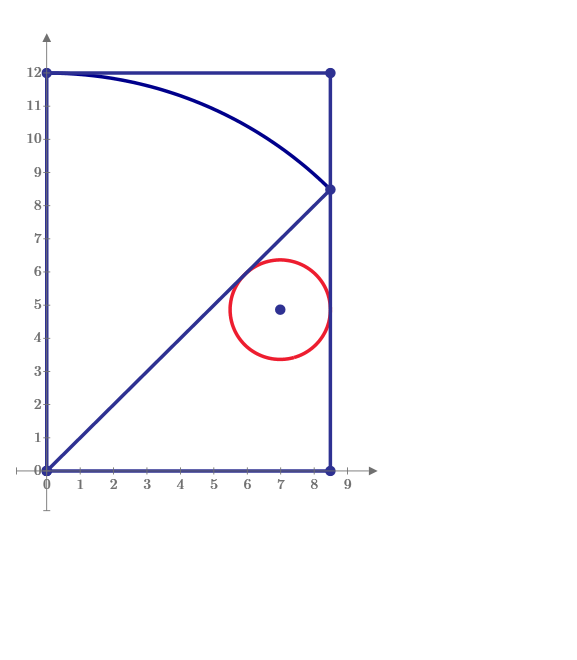
Thanks, challenge this puzzle. θ=90 degree is the Entrance Exam of High school in Japan. It requires the position of cap and the length of role paper with minimum length. My answer of the one of 45 degree is here. l=12/sqrt(2).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm,
Note that the cone height is not specified.
When cone and cap have 'largest areas' (possible, given the width of the paper roll)
I get this for theta=45 deg:
And here the paper length required is 12 *sqrt(2).
The smaller theta, the longer the paper required...
But also, the higher the cone.
Success
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your result is true. The original puzzle is fixed 90 degrees and the position and radius of cap is the problem.
So, use 12 cm width of roll paper and minimize the required length is the problem I want to say.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
Your result is true. The original puzzle is fixed 90 degrees and the position and radius of cap is the problem.
So, use 12 cm width of roll paper and minimize the required length is the problem I want to say.
"required" for which goal?
The problem needs some sort of additional specification.
I see two possible options:
1) You may ask for a cone with maximum surface (cone plus circle) and the minimum paper consumption for it. This is how Luc (and me, too) interpreted your puzzle, however, this approach contradicts your solution for 45°.
2) You may ask for a cone with a constant side length of 12 cm and minimal paper consumption. However, this approach contradicts the table you showed in your initial post. Using this interpretation a maximum angle of 180° would be allowed, but your table showed a solution for 360° (two circles with radius 6).
Furthermore you wrote about the "center angle" of the cone but it seems to be clear that you rather meant the angle in the net we get when we unroll the cone.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I want to make this puzzle as your 2).
Cone side must use 12 cm width of roll paper.
So, if the angle is close to 0-degree, Cone seems to y axis 12 cm. And cap seems to point.
If the angle is close to 360-degree, Cone seems to circle with radius 6 cm and the cap is also same circle as you mentioned above.
This is my answers I got. Blank answer is already calculated but not shown to fun of this puzzle. (Or want more minimum length of roll paper to need.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmmm, it is of course your puzzle and so you also set the rules, but I find it quite illogical to let the cone sides become shorter than 12 cm for angles above 180°, but to insist on the length 12 cm for angles below 180°, although a greater length would also be possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
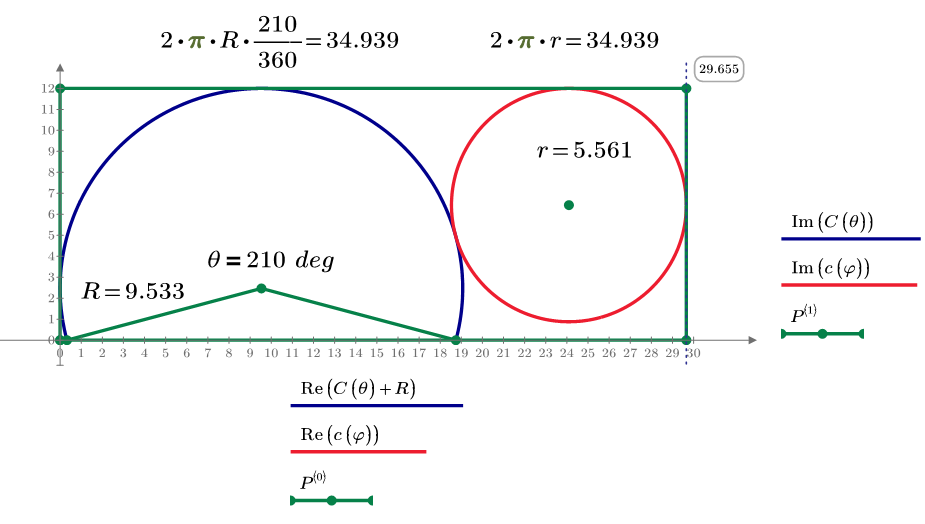
My answer of θ=210 degrees. Using 12 cm width and minimum l=29.655 cm.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I understand what you do. I just think its inconsistent to forbid making the cone larger than 12 cm side length (like in Lucs 45° solution) but accept to make it smaller for angles larger than 180°. Just my 2 cent.
I would rather stay with "largest surface but minimal paper" throughout or with constant side length 12 cm and minimal paper (which would allow only angles from 0 to pi.
Here a numerically derived solution for the latter:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. Please share your worksheet. This is what I want to solve. The function is not linear or simple function but have many turning points. 😀
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here you are, but you will be disappointed as the sheet is not only bit of a mess but the paper lengths are not really calculated 😉