Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Find() works but not solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find() works but not solve
To all experts,
I am breaking down an investigation I am hoping to do to simple blocks. I am looking at creating “dummy” bi-modal PSDs to meet a specific rms value. See attached mcad15 sheet
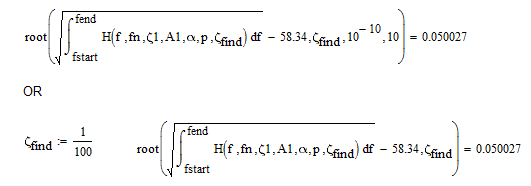
If I specify the values fn, zeta1, A1, alpha and p is there a way of Mathcad finding the zeta2 value required to get a given rms value? A solve is returning “no solution found” but it works with a Find(). I believe one cannot use Find() in a program
Ultimately, I would like to create a number of f dummy PSDs with the same (or near) rms value by changing the parameters. For example, I would like to specify a series of alpha values and get a vector of rms value
Thanks
Regards
JXB
Solved! Go to Solution.
- Labels:
-
Programming
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic "solve" tries to give you an exact result, so it first tries to integrate symbolically which it obviously is not capable of - thats the reason it finds no solution.
Fortunately you are looking just for numeric results and so you definitely should use Mathcads numeric methods like the solve block you had implemented or one of the two flavors of the "root" command:
You sure can use a solve block or the "root" command in a program. You should turn them into a function of the variables you wish to change and in case of the solve block you may even add the guess value as argument of that function.
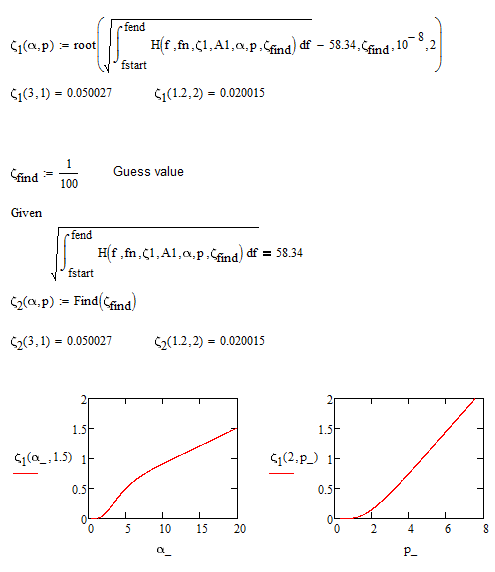
The attached worksheet shows how to do that and somehow I got the impression that the function zeta.1 based on the root command works faster than zeta.2 based on the solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic "solve" tries to give you an exact result, so it first tries to integrate symbolically which it obviously is not capable of - thats the reason it finds no solution.
Fortunately you are looking just for numeric results and so you definitely should use Mathcads numeric methods like the solve block you had implemented or one of the two flavors of the "root" command:
You sure can use a solve block or the "root" command in a program. You should turn them into a function of the variables you wish to change and in case of the solve block you may even add the guess value as argument of that function.
The attached worksheet shows how to do that and somehow I got the impression that the function zeta.1 based on the root command works faster than zeta.2 based on the solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot for the solution. Another block sorted.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
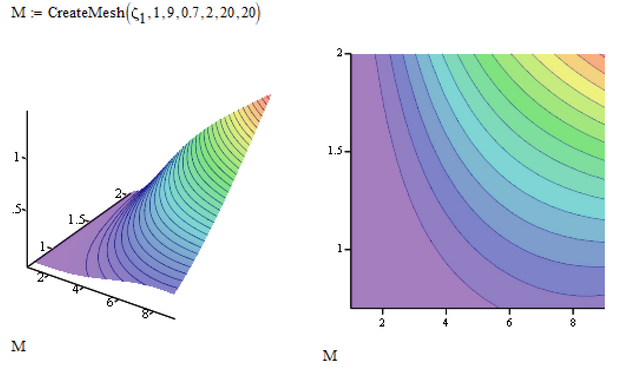
Playing with some alpha & p parameters. Would there be a way of plotting a surface plot (x,y,z)=(alpha,p,zeta2)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@JBlackhole wrote:
Playing with some alpha & p parameters. Would there be a way of plotting a surface plot (x,y,z)=(alpha,p,zeta2)?
Sure! zeta.1 and zeta.2 already are functions of the two arguments, so you may 3D-pot them directly, but I'd rather suggest using CreateMesh for better control about the ranges of input variables.
Unfortunately the calculation is quite sensitive to the ranges of alpha and p. As soon as the calculation fails for just one combination of alpha and p, the whole plot fails.
zeta.1 may fail because of the interval I had chosen (10^-8 to 2). function values at the start and at the end of that interval must have opposite sign.
zeta.2 may fail because of the guess value not being optimal for the chosen arguments.
You have to experiment a bit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks. Yes I have noticed the sensitivity hence me playing with the data. I think I have have almost a range of realistic value as I added another block to my problem and it seems to work
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This cannot be solved symbolically. But... Are you sure your definition of H is correct?
In the denominators you are adding r1^4 to r1^2. That should throw an error if r1 has units (I suppose it hasn't, because r1 is the ratio of f and fn), but still...
Needless to say: if that first term under the root would be (1-r1)^2 or (1-r1^2) the integral would easily solve symbolically.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Appreciate I put this together quickly last night but it seems correct to me. The "famous" transmissibility for a 1-DoF model