Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Find x value for max(y)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find x value for max(y)
Hi, I have a function y[x which behaves as an inverted parabola. By using the command max(y) I can find the maximum y value, but I would also like to find the associated x value. What command can I use to find the x value? Thanks!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
J M schrieb:
Thank you, In my case however the 'x' term is not in matrix form, it is a series. Please find the attached file to see the problem. I know that the maximum point can be found by setting the derivative of the function equal to zero but this will be impossible as the model grows in complexity.
As you do not want to turn your vector E into a function and use the derivative you have at least two options:
1) turn x into a function and use the method I had posted
2) use "match" to get the index if the maximal value which in your case would be the searched for x value, too.
See attached worksheet for details.
Edited: haven't realized that Stuart already had posted.
I second his remark about not giving up on the function approach. At the end of my worksheet you find a symbolic solution using functions. If the functions get more complex and the symbolic solver is not able to find a solution you would resort to a numeric solution by using a solve block.
have just updated the file and included a solve block and the root function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There may be a lot of ways to do this. One is to set f(x)=max_y in a Given - Find(x) block. Use the Boolean =. The max_y may need to be obtained from an earlier operation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think what you a looking for is the "lookup" function in Mathcad.
For future questions keep in mind that you will get a better response from the community if you attach a worksheet (upper right corner, extended editor). It also makes sense stating which version of MC you use.
From what you wrote I assume that you have two vectors, x and y.
What you need is something like x_max:=lookup( max(y), y, x )[0
Another solution would use the "match" command y[match(max(y),x)[0
Remember that match returns the index - in the screenshot below ORIGIN was 0, so index 2 is the third position.
lookup and match return vectors as there may be more than one occurence (as in the example below). Thats the reason for the "]0" in the two expressions above, assuming you want the first occurence of the max (and ORIGIN is left at 0),

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, In my case however the 'x' term is not in matrix form, it is a series. Please find the attached file to see the problem. I know that the maximum point can be found by setting the derivative of the function equal to zero but this will be impossible as the model grows in complexity.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
J M wrote:
Thank you, In my case however the 'x' term is not in matrix form, it is a series. Please find the attached file to see the problem. I know that the maximum point can be found by setting the derivative of the function equal to zero but this will be impossible as the model grows in complexity.
You simply need to convert x into a vector (or create another variable based on x), eg
xx[x:=x
You can then use Werner's suggested method
lookup(E.max,E,xx)
However, you will face a slight problem here as E is sufficiently flat near the top of your curve that several values of E meet the default criterion of E.max. You will have to reduce TOL (eg, 10^-5) to get an answer.
Don't write off the derivative method just yet. You many find either the symbolic or numeric solve blocks can give you correct value ... the lookup method is constrained by the limited set of E values that can be generated as result of the step size of x
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
J M schrieb:
Thank you, In my case however the 'x' term is not in matrix form, it is a series. Please find the attached file to see the problem. I know that the maximum point can be found by setting the derivative of the function equal to zero but this will be impossible as the model grows in complexity.
As you do not want to turn your vector E into a function and use the derivative you have at least two options:
1) turn x into a function and use the method I had posted
2) use "match" to get the index if the maximal value which in your case would be the searched for x value, too.
See attached worksheet for details.
Edited: haven't realized that Stuart already had posted.
I second his remark about not giving up on the function approach. At the end of my worksheet you find a symbolic solution using functions. If the functions get more complex and the symbolic solver is not able to find a solution you would resort to a numeric solution by using a solve block.
have just updated the file and included a solve block and the root function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The reason I didn't post a worksheet showing what I meant was that I wrote a symbolic solution ... then, whilst trying a slightly different variant, typed something that caused my worksheet to disappear like money into a lawyer's pocket.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff schrieb:
The reason I didn't post a worksheet showing what I meant was that I wrote a symbolic solution ... then, whilst trying a slightly different variant, typed something that caused my worksheet to disappear like money into a lawyer's pocket.
Stuart
Good to see that I am not the only one with experiences like that.
Like the lawyer comparison 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, that did the trick!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you have a function, take the derivative of it and solve for the root.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
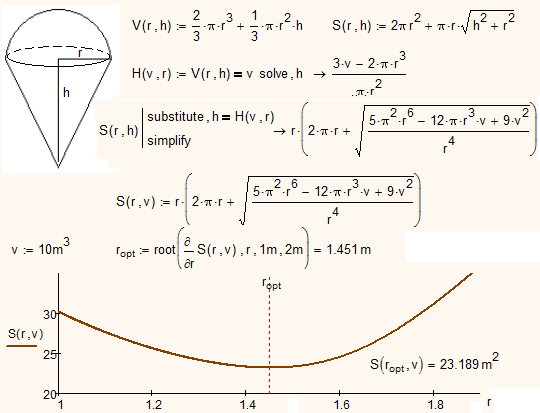
Fred Kohlhepp wrote:
If you have a function, take the derivative of it and solve for the root.
One good example:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator






