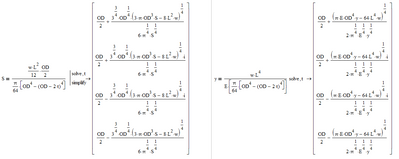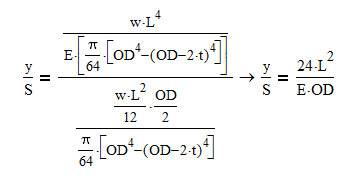Finding one value given two constraints

[NovaStark]

Hi all,

I have the need to use a MathCAD function (possibly) but I am not sure how to achieve what I would like the program to try to do.

My situation is essentially I havea fixed-fixed beam of circular cross section with a known span L anda uniformly distributed load w.

So using standard beam equations I have the max moment is M = wL^2/12 so the max stress is S = [(wL^2/12)(OD/2)]/I

where I = (pi/64)(OD^4-ID^4), OD is known

and the max deflection is y = wL^4/384EI where E is a known constant.

What I would like to eventually find is the thickness t = 0.5*(OD-ID) which just satisfies y = 0.1 and S = 2000.

Usually by hand, I would work use S = 2000, find the value of I and work out ID, then find t, substitute into the formula for y and see if equal to 0.1. I can probably assess it graphically but that would probably not give me too exact of an answer.

However I am not sure what functions would help me get MathCAD to automate this for me. Can anyone shed any light on how to go about doing this ?

[LucMeekes]

Like this:

Note that I is the same value, for each of the four solutions, the second solution gives a negative ID and the last two of the solutions for ID are pure complex (imaginary) numbers. 

Success!
Luc

[LucMeekes]

Update

[terryhendicott]

Hi,

With realistic engineering units and values.

It is not possible sometimes to meet both a "y" and an "S" limit.

Cheers

Terry

[Fred_Kohlhepp]

As Terry indicates you may not be able to satisfy both equalities at the same time.  I rewrote your equations for y and S putting in t (ID = (OD -2t).  If I divide S by y I can get:

You can solve either equation of S or y for t:

Whichever is more critical will depend on the actual problem.

[NovaStark]

Thanks that makes sense. But would I be able to find the first value of t that satisfies S= a fixed value with y < 0.1 ?

[Fred_Kohlhepp]

Depending on the problem one of your two limits will be more restrictive than the other.  You can derive an expression between y and S that does not involve the thickness:

The attached sheet gives a starting point.  (In my experience, designing for deflection is usually more restrictive than designing for stress.