Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Finding the constants of an ODE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finding the constants of an ODE
Hello everyone,
I have the differential equation m∙x ̈+C∙x ̇+k∙x=0 and i know only the mass, do you know if there is a way to find the coefficients C and K? do you think this can be solved with odesolve if i declare some initial conditions?
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Iulia Savu wrote:
Hello everyone,
I have the differential equation m∙x ̈+C∙x ̇+k∙x=0 and i know only the mass, do you know if there is a way to find the coefficients C and K? do you think this can be solved with odesolve if i declare some initial conditions?
I'd be interested to see any answers to this showing how, but I don't think you can. AFAICT, if you know the mass and initial values (eg, position, speed), then you will still need to know what C and k are to know how the system will evolve. For example, if I attach a weight to the bottom of a (massless) spring, and pull it down, then I won't know how quickly the spring will pull it back up unless I know how strong the spring is. You may have a chance if you know the final values as well, though.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So how do I find C and k, given m, x(0) and x'(0), Valery?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Two equs with two unknowns
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Two equs with two unknowns
Guess no! The two initial conditions were already used to derive the solution which Wolfram came up with.
You can't use them a second time. Those two equations would be true for any valid value of k an C.
Its like Stuart already said - mission impossible!
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As Werner says, no. You start with a differential equation with 5 unknowns: you do not know x, x', x'', C, or k. Given two initial conditions you can turn that into a non-differential equation in three unknowns: at a given t you do not know C, k, or x(t). Without more information, that is where it ends. It's not solvable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And what do you think about the answers bellow? can i get real values for K and C if a have 4 initial conditions?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You don't need 4 initial conditions. Two initial conditions are enough to get rid of the derivatives, as Valery has shown (Mathcad can't do what Valery showed, but a solution is a solution ![]() ). Once the derivatives are gone, you just have an equation that is a function of t with two unknown constants. If you know the values of x(t) for any two times, t, then you can find C and k. So you need 4 conditions, but only two of them need to be "initial" conditions.
). Once the derivatives are gone, you just have an equation that is a function of t with two unknown constants. If you know the values of x(t) for any two times, t, then you can find C and k. So you need 4 conditions, but only two of them need to be "initial" conditions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Iulia Savu wrote:
And what do you think about the answers bellow? can i get real values for K and C if a have 4 initial conditions?
I think there may be some confusion in the thread about what comprises an "initial" condition.
I assume that by an initial condition you mean some piece of information that is known at just one value of x rather than something that is known at some other value of x as well (eg, just x1, rather than x1 and x2)?
What 4 "initial" conditions do you think you might have?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
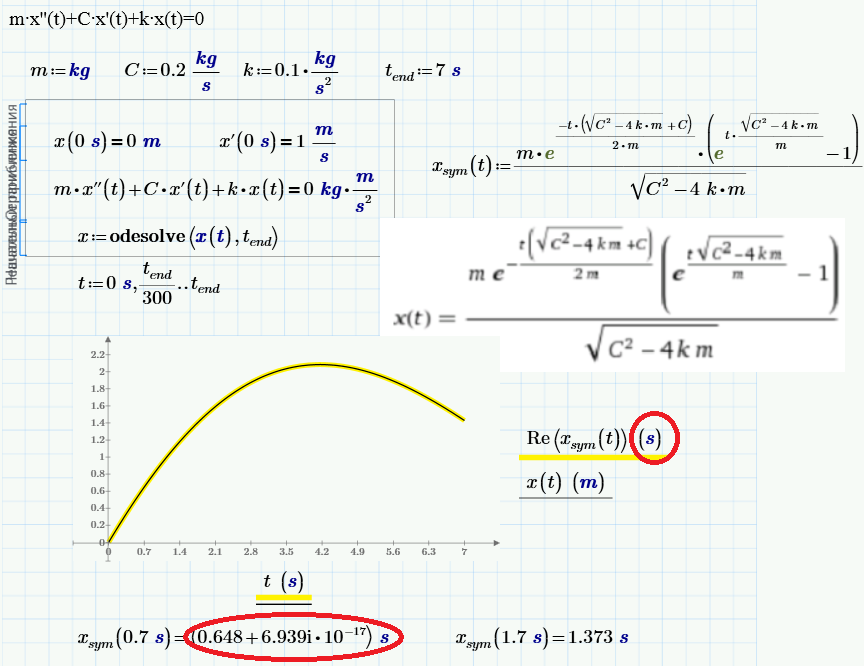
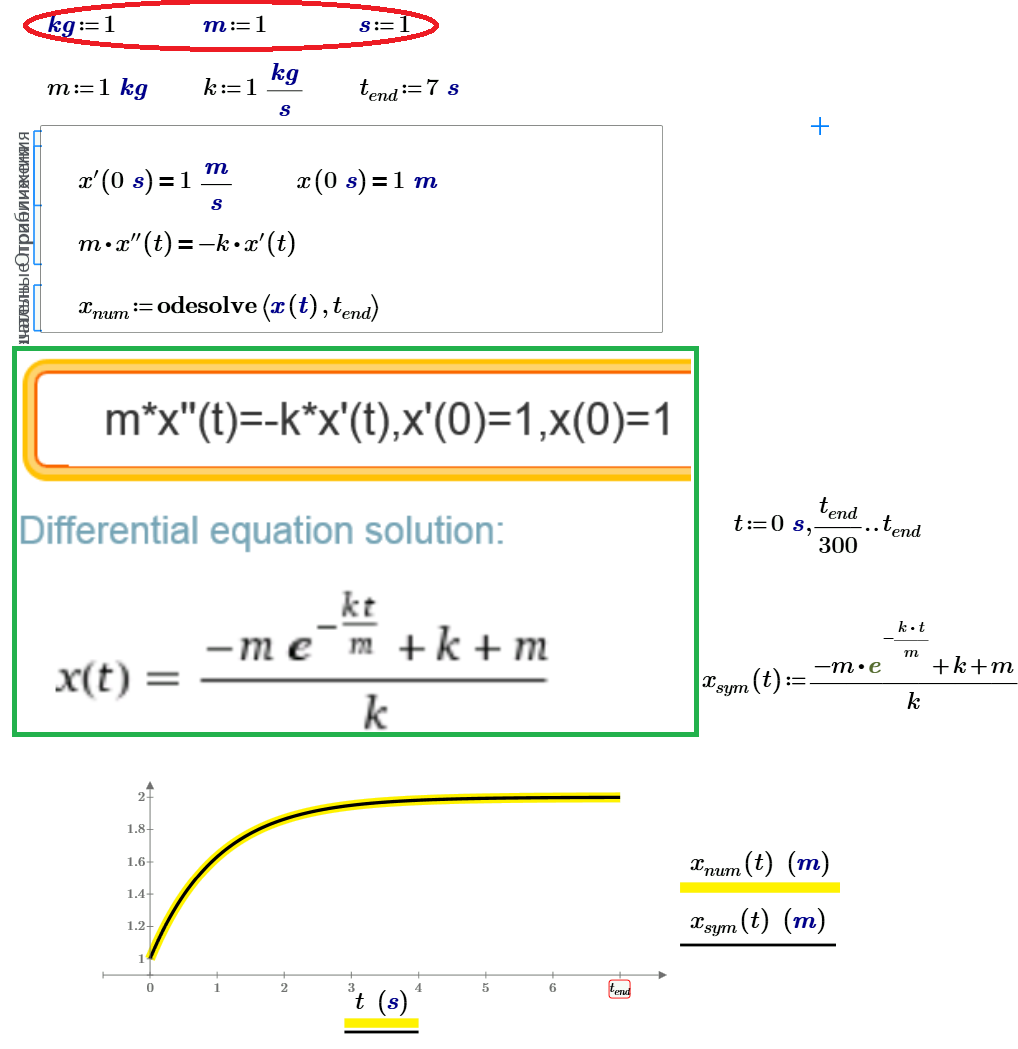
Sorry, only so we can compare num and sym ODE Solutions with "units":
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Knowing the general integral of the differential equation and some initial conditions, it is possible to determine the coefficients P and Q , in your case, C and k.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So i need to use the case of real roots, because i need real values that are going to be used later as parameters, and i don't understand how am i going to extract the values of c1 and c2 . Do i use the initial conditions? Because i don't think that's going to work...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Iulia,
you need four initial conditions:

If you know as initial conditions even the first derivatives, then the road to the solution is a bit different.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Lulia.
You can combine an Odesolve block with a Find one.
Best regards.
Alvaro.
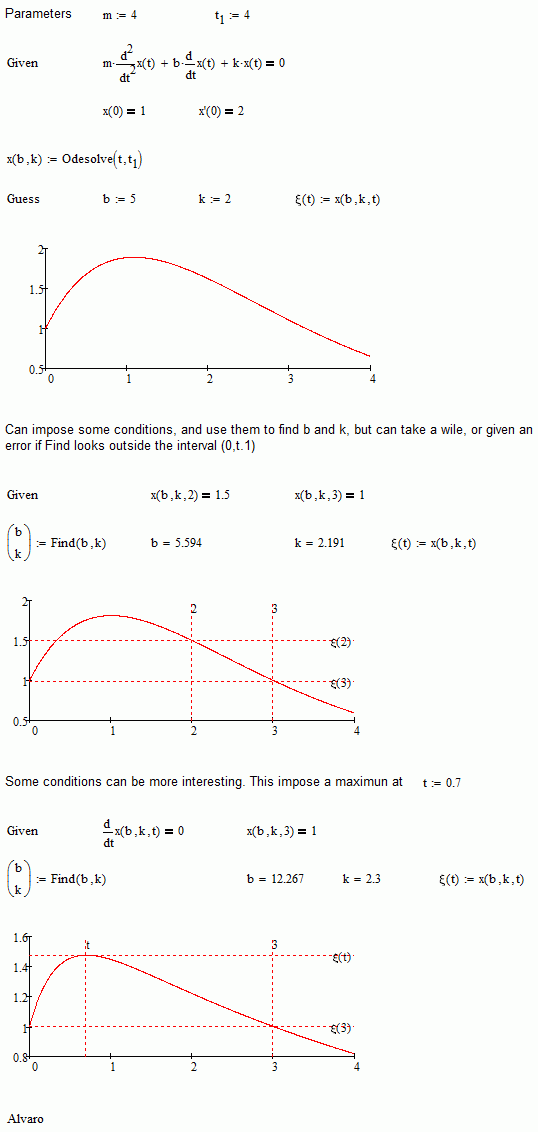
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alvaro!
Yes - "Two equs with two unknowns" - see above.
But better in Prime with units: m:=4 kg etc