Finding the constants of an ODE

[isavu]

Hello everyone,

I have the differential equation m∙x ̈+C∙x ̇+k∙x=0 and i know only the mass, do you know if there is a way to find the coefficients C and K? do you think this can be solved with odesolve if i declare some initial conditions?

[StuartBruff]

Iulia Savu wrote:

Hello everyone,

I have the differential equation m∙x ̈+C∙x ̇+k∙x=0 and i know only the mass, do you know if there is a way to find the coefficients C and K? do you think this can be solved with odesolve if i declare some initial conditions?

I'd be interested to see any answers to this showing how, but I don't think you can.  AFAICT, if you know the mass and initial values (eg, position, speed), then you will still need to know what C and k are to know how the system will evolve.  For example, if I attach a weight to the bottom of a (massless) spring, and pull it down, then I won't know how quickly the spring will pull it back up unless I know how strong the spring is.   You may have a chance if you know the final values as well, though.

Stuart

[ValeryOchkov]

[StuartBruff]

So how do I find C and k, given m, x(0) and x'(0), Valery?

Stuart

[ValeryOchkov]

Two equs with two unknowns

[Werner_E]

Valery Ochkov wrote:

Two equs with two unknowns

Guess no! The two initial conditions were already used to derive the solution which Wolfram came up with.

You can't use them a second time. Those two equations would be true for any valid value of k an C.

Its like Stuart already said - mission impossible!

Werner

[RichardJ]

As Werner says, no. You start with a differential equation with 5 unknowns: you do not know x, x', x'', C, or k. Given two initial conditions you can turn that into a non-differential equation in three unknowns: at a given t you do not know C, k, or x(t). Without more information, that is where it ends. It's not solvable.

[isavu]

And what do you think about the answers bellow? can i get real values for K and C if a have 4 initial conditions?

[RichardJ]

You don't need 4 initial conditions. Two initial conditions are enough to get rid of the derivatives, as Valery has shown (Mathcad can't do what Valery showed, but a solution is a solution ). Once the derivatives are gone, you just have an equation that is a function of t with two unknown constants. If you know the values of x(t) for any two times, t, then you can find C and k. So you need 4 conditions, but only two of them need to be "initial" conditions.

[StuartBruff]

Iulia Savu wrote:

And what do you think about the answers bellow? can i get real values for K and C if a have 4 initial conditions?

I think there may be some confusion in the thread about what comprises an "initial" condition.

I assume that by an initial condition you mean some piece of information that is known at just one value of x rather than something that is known at some other value of x as well (eg, just x1, rather than x1 and x2)?

What 4 "initial" conditions do you think you might have?

Stuart

[ValeryOchkov]

Numerical  and Symbolical (Wolfram) Solution with units - ???

[ValeryOchkov]

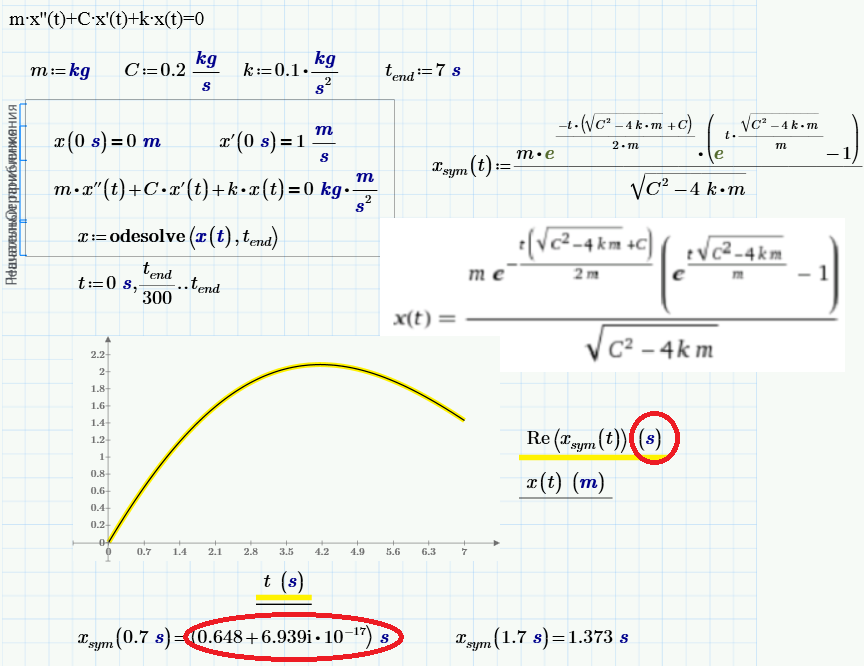
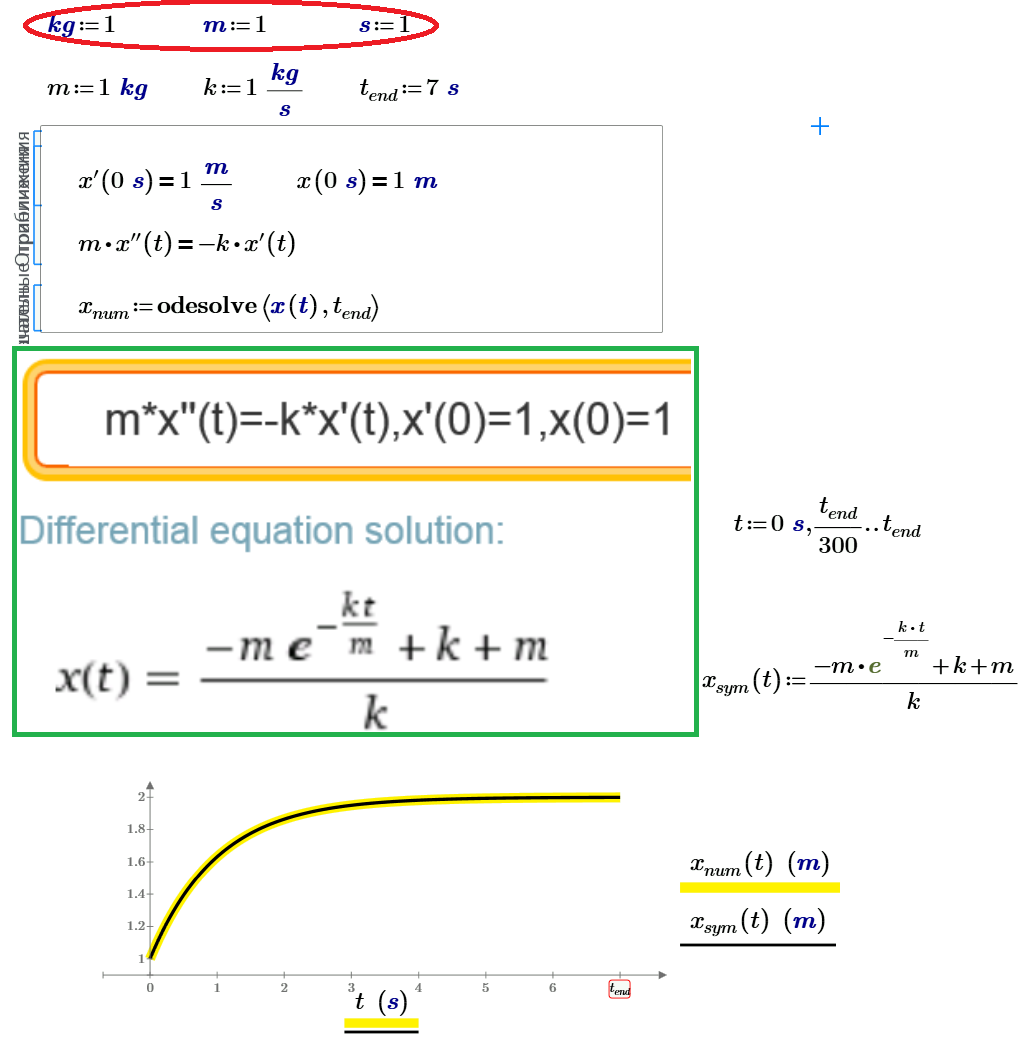
Sorry, only so we can compare num and sym ODE Solutions with "units":

[-MFra-]

Knowing the general integral of the differential equation and some initial conditions, it is possible to determine the coefficients P and Q , in your case, C and k.

[isavu]

So i need to use the case of real roots, because i need real values that are going to be used later as parameters, and i don't understand how am i going to extract the values of c1 and c2 . Do i use the initial conditions? Because i don't think that's going to work...

[-MFra-]

Hi Iulia,

you need four initial conditions:

If you know as initial conditions even the first derivatives, then the road to the solution is a bit different.

[AlvaroDíaz]

Hi Lulia.

You can combine an Odesolve block with a Find one.

Best regards.

Alvaro.

[ValeryOchkov]

Thanks, Alvaro!

Yes - "Two equs with two unknowns" - see above.

But better in Prime with units: m:=4 kg etc