Fitting an Ellipse to a Blob (re-post?)

[MoeSzyslak]

Collab --

In the attached worksheet, I am attempting to fit an ellipse to a blob. I believe that the fitting orientation is correct, but it appears that my scaling is somehow off. I can calculate the area three ways -- pixels in the blob, using ellipse semi-axes, and integrating the function (but how?) -- and I would expect all of these values to be similar. From visual inspection, they are not. What am I missing?

Apologies in advance if this is a re-post -- I tried to submit yesterday and got a message that a moderator had to approve it first. I have never seen that message before and it has now been 24 hours, so I suspect that the original post may be in the ether, but I'm not sure....

Matt

[AlanStevens]

In your definition of p shoulodn't you replace P/root(n) by augment(A,B)?

Alan

[MoeSzyslak]

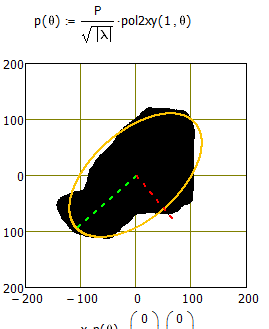
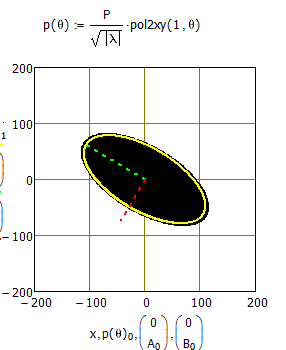
Alan -- very nice. That is indeed the ellipse defined by the semi-axes shown, but its area is much larger than the blob. So, you have reconciled two of the sizes, but not the third. Thanks!

[Werner_E]

You ar perfectly right, Alan, but unfortunately B seems to be wrong. I tested it with a couple of perfect ellipses and A was perfect in every case, but B was always to far away from center.

Its crazy - we are still moderated and now Im even not given the opportunity to edit my post below.

[RichardJ]

The moderation is due to some spammers flooding PlanetPTC with junk. I'll refrain from saying what I think of them, because then the moderator wouldn't allow my post

The equations you are using to draw the ellipse and the axes clearly do not match. The axes are for a much bigger ellipse than the one you have drawn, one that would encompass all, or at least nearly all, the pixels. That's why the area is much bigger than the image area. I can't tell you where the problem with your equations is though without going back to my geometry books.

What is the end goal of this? There is more than one way to fit an ellipse to data, and the best choice will depend on what you are trying to get from that ellipse.

[MoeSzyslak]

The 'blob' represents a feature in an image. I scan through the image, extract all blobs, and then fit ellipses to them as a means to quantify their orientation and size. I can then analyze the collective by means of (e.g.) a polar histogram, to which I can fit a truncated Fourier series, which provides me with a measure of preferred orientation and degree of anisotropy.

[RichardJ]

This will give you what you want. The size of the ellipse is quantitatively defined in terms of the standard deviations along the principal axes of the blob. If the layout looks a little odd (especially the change in variable names in some places) it's because I adapted the worksheet from one I already had. You can clean it up

[MoeSzyslak]

Richard -- very helpful, as always. Thank you for the worksheet. I think I follow what you've done -- I was trying to do a 'short-circuited' PCA myself, but clearly came off the rails somewhere. That said, I still wish I could figure out why the scale of my ellipses is incorrect....

[RichardJ]

-- I was trying to do a 'short-circuited' PCA myself, but clearly came off the rails somewhere.

Given the eigenvector approach I thought that might be the case.

I still wish I could figure out why the scale of my ellipses is incorrect....

Maybe if you lay out my math next to yours and try to reconcile the results you get at each step you could figure that out.

[Werner_E]

While better still sure not the correct scaling. Think its agood idea to test with the pic of a perfect ellipse.

[MoeSzyslak]

Interesting. Also, very smart to test the algorithm with an actual ellipse. I should have thought of that....