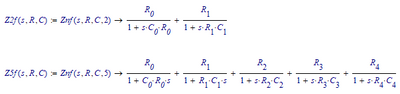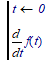Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Foster to Cauer Conversion
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Foster to Cauer Conversion
I am trying to write a program that implements the Foster - Cauer conversion algorithm described in summarily in page 19 of System-Level Thermal Simulation - nxp.com and thoroughly in appendix 2 of Aliyu, Attahir Murtala PhD thesis (that also includes an implementation in MATLAB) , but I cannot find how to program the manipulations they describe using MathCAD, especially the "polynomial long division" to obtain "quotient + remainder".
Anyone willing to help?
Note that I am using MathCAD 15
Thanks
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't have v15, but I have a reasonable guess. If you look at the beginning of the Z2RCladder area, I define a function Stack, which accepts NaN (not a number). This acts as a NULL number. V11 allows for it; I don't know if v15 does or not. In any case, the object of Stack is to allow use of cases such as Stack(NaN, vec), which simply returns vec, the non-NaN argument. The built-in function stack in v11 gives an error in this case; it requires both arguments to be arrays of appropriate dimensions. I don't know if this hold true in v15.
This behavior is useful when iterating calculations through a number of values, and want to append the result of the most recent cal to the existing array. By setting the initial value to NaN, the the initial calc (with no preceding calc values to append to) does not need to be treated/programmed as a special case.
If you can find an alternate way to implement Stack, then simply replace my original definition. The revised file attached goes another route.I implemented a second version of the Z2RCladder function, in which I initialize the RC array to (0 0) instead of NaN. This results in an extraneous first row in the output array, which is removed before returning the RC values.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
the following two photos illustrate the algorithm of the synthetic division and an example (you have only to change z with s):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Topaz,
Thanks for your reply but this is not exactly what I am looking for. It is not as simple as replacing z with s.
To find the Cauer parameters the quotient of each iteration gives the value of one component and the remainder is used for the next iteration.
I attached a MathCAD file that implements the example A2.3 of Aliyu, Attahir Murtala PhD thesis .
This example is for a second order Cauer network with two capacitors and two resistors. It can easily be expanded to higher order but the problem is that I need to do this calculation for several thousands of networks then I need to convert this into a MathCAD program that I can call each time I need to find the Cauer parameters of a network.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Are all your filters the same size (Same number of R's and C's, same topology)?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes they will be 5th order Cauer networks like this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So you have this:
Which means that, for a 2 and a 5-stage network you get, respectively:
Then with Mathcad 11 you can:
With this you have to divide the numerator out in every division, to get the numerators to 1.
Unfortunately Mathcad 11 will not give the full symbolic solution for a 5-stage network (it does 3, tries 4 but takes an awefull lot of time), but:
If the numbers are known, a solution is found.
As said, this works in Mathcad 11, I don't think it will work in mathcad 15, nor in any existing version of Prime.
This probably is the way it can be solved:
Wherein the construct:
Means 'the result of the 1st derivative of f to its argument, at the point where the argument is 0'.
I hope this gets you a step further.
Success!
Luc
P.S. Mathcad 11 actually does the 4-stage fully symbolically, but the result is uncomfortably big.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Laplace domain, the network looks like this in MathCAD 15:
You can see by looking at the left side, that the technique of "quotient + remainder" is probably the easiest way to retrieve the values of the Cauer network.
But doing the symbolic manipulation in a MathCAd routine, that I didn't find how to do it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm getting close, but not completely there:
For the example of the Thesis this gives:
Which is correct (please check!).
There's an 8-section example in the NXP presentation that goes completely off.
There's one remark to make already: since I'm using multiple symbolic assignments in one program, chances are that this will not work in any other than Mathcad 11.
But it may be possible to find a similar approach that does work in Mathcad 15.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It looks like this is why I cannot do it.
I need to male multiple symbolic assignments in my program and it is not possible in MathCAD 15!
I just called PTC support and they said that it is not possible to download MathCAD 11.
Is there an other way to get it?
I will try to call PTC support to see if they can find a way to do that in version 15.
Thank you very much anyway, I would not have found why I can not do it without your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hang on a little more.
It's not completely lost, even for Mathcad 15.
Note that the function NUmDen2Cauer, which does most of the work, does NOT use symbolics. It just needs the coefficients of the Numerator and the Denominator polynomes. How it gets it (or, how you get them in there) is another matter. In my (Mathcad 11) case it is essentially what Foster2Cauer does, just before it calls NumDen2Cauer.
Most important at this time is to find the error that is apparently in NumDen2Cauer. I didn't find it yet.
For implementation of that function I used this source: https://nl.mathworks.com/matlabcentral/fileexchange/48042-foster-and-cauer-equivalent-networks (under the "Function" tab). I'm not fluent in Matlab: I may have made a mistake in my implementation, or there is a mistake in that algorithm.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
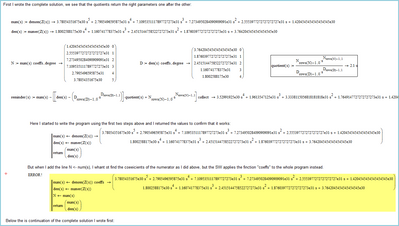
In the file attached, I tried to write the program and if fails when I insert the command to extract the coefficients:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attached is the same file but saved as MathCAd 11
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I had done work on routines for impedance manipulation some time ago (as may be seen in the age of some of the included functions), when I was also working on thermal models. I cleaned an old file that did the desired conversion so it is self contained. Only a few of the polynomial functions are needed, but I left them all in case others may be interested. I have not reviewed the main impedance programs; they are what I had done some years ago.
This is a v11 program - I'm one of the remaining users keeping an old PC going just for this reason. It should work in v15, since the routines are numeric and don't depend on symbolics, except for a few simple function examples.
It gives the same answer for the 8th order as the NXP paper.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For some reason, I couldn't add a second attachment in the previous post Here's a pdf, but it doesn't show the heavy lifting.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Lou,
Thanks for posting your file, it contains a lot of useful functions.
When I run it, MathCAD 15 returns an error and here is the trace I did:
Can you explain what is wrong?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't have v15, but I have a reasonable guess. If you look at the beginning of the Z2RCladder area, I define a function Stack, which accepts NaN (not a number). This acts as a NULL number. V11 allows for it; I don't know if v15 does or not. In any case, the object of Stack is to allow use of cases such as Stack(NaN, vec), which simply returns vec, the non-NaN argument. The built-in function stack in v11 gives an error in this case; it requires both arguments to be arrays of appropriate dimensions. I don't know if this hold true in v15.
This behavior is useful when iterating calculations through a number of values, and want to append the result of the most recent cal to the existing array. By setting the initial value to NaN, the the initial calc (with no preceding calc values to append to) does not need to be treated/programmed as a special case.
If you can find an alternate way to implement Stack, then simply replace my original definition. The revised file attached goes another route.I implemented a second version of the Z2RCladder function, in which I initialize the RC array to (0 0) instead of NaN. This results in an extraneous first row in the output array, which is removed before returning the RC values.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It works!!!!
This will make me a disciple of your polynomial function library 🤓
Thanks a lot!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice Lou !
I guess you've solved the problem of the OP, if the files runs in Mathcad 15 as well.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
Can you post the v11 program that has your NumDen2Cauer() function?
Probably a brain freeze, but not sure I understand what you mean by OP.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sure, here she is.
Brainthaw: OP=Original Poster.
Luc
You can only attach one file to a (new) post or answer. To attach a second file, you have to edit your existing posting...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
You can only attach one file to a (new) post or answer.
Not exacly true. You CAN attach multiple files already in your first attempt but they must all be marked/highlighted at once. Once you have attached a file (or a couple of files) you cannot add more attachments but must post your answer and then edit it again.
Annoying anyway
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess you're right.
Thanks!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See if this works better.
Note: You ARE able to get arrays with the coefficients of the numerator and the denominator. That should be all that is required. As I said. The important work is done in the NumDen2Cauer() function, which only requires the two arrays with coefficients...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
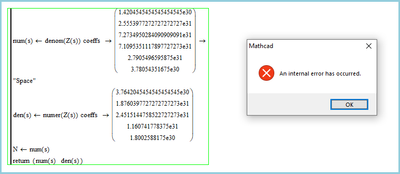
Hi Luc,
This produces an internal error:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
I think that all the math in your function NumDen2Cauer is correct. Also, the submatrix operations throw out the terms that are expected to be zero, so any nonzero residual value from incomplete cancellation doesn't matter. This function and my implementation agreed in all cases when given the same coefficient vectors. To be completely general, you could allow for the cases 1) that have an input resistance & no shunt capacitance, resulting in num and denom polynomials having the same order. The routine as is doesn't allow for this. Need to jump to the R calc as the first value calculated, then resume with C-R-C-R..., and 2) where there is no shunt R at the end (DC open circuit, or Rend = infinity). In this case, the den polynomial has zero constant term, so Z has a pole at s=0.
The calc errors come from the symbolic calculation of the num and denom coefficients. I set up your symbolic function which just returns the coefficients, and did not include the NumDen2Cauer function. Strangely, for cubic or higher order polynomials, the set of coefficients for a polynomial is correct, but they appear in an incorrect order - they are permuted.
I played with splitting up the symbolic calc, and wound up with a sequence I call step-by-step symbolics (see images). This worked for all the examples I tried, up to the eighth order example. In the image, the errors for a third and fourth order terms can be seen in the one step calc, while the step-by-step symbolics and my numeric calc give the correct answers.
One observation concerns me. Using the real (decimal) values of the eighth order example, the symbolic coefficients get quite big, ~10^85. I guess that the symbolic engine is converting the real numbers to rational fractions and working from there. I have found a few simple decimal RC inputs for which the coeff calc didn't work at all.
The v11 file with the new examples is attached.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much Lou, for sorting that out.
I've trusted the symbolic results too much. Now, once more, this shows that it is hard, to impossible, to control the output (shape) of symbolic results. That can have, and in this case has, a serious impact on obtained results.
Thanks!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
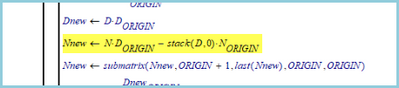
Is it possible that your result goes off because the subtraction
does not cancel completely the largest exponent.
I had that problem and here is what I did:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Could be.
The statement is my (Mathcad) implementation of the Matlab: Nnew = N*D(1)-[D 0]*N(1);
It would mean that the source is incorrect...
Thanks!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
I don't think the source is incorrect.
In the highlighted line, I calculated the reminder and the s^5 should have go away but It didn't because of floating point residues. In the next line, to work around, I used the s^5 of the numerator plus the denominator minus its s^4 times the quotient, in the calculation of the reminder.
I thought that maybe the same thing happened in your file at: