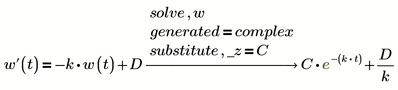Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Getting the wrong answer from an integral
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Getting the wrong answer from an integral
Mathcad Prime 9.0.0.0
I'm doing a separation of variables equation, where I start with the equation at the top left in the screenshot. Using the solution that mathcad provides from the integrals, i get an output, that doesn't match up with the true answer (highlighted in blue). Am I using it wrong?
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The C in your solution and the C in the highlighted solution are different constants of integration! The differ just by the sign, so this should not be any problem.
To be precise, the constant of integration stems from the first time you integrate the equation -> +C1 and C1 is any reals number.
When you now de-logarithmize it gets C=exp(C1) and now C only can be positive!!!
But because the integration of 1/x actually is ln (|x|) (note the absolute value), at the end C can be chosen any real number.
BTW, Prime can solve the simple ODE in one go:
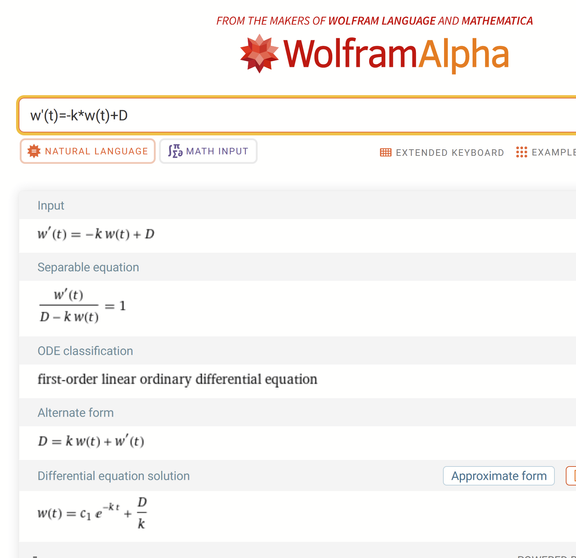
The sign of the constant C does not matter. I could as well have substituted _z (thats the name of the variable generated by Prime originally) by -C to get the solution you highlighted.
BTW, even though it doesn't mean anything, the solution of Wolfram Alpha also uses the same sign convention
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The C in your solution and the C in the highlighted solution are different constants of integration! The differ just by the sign, so this should not be any problem.
To be precise, the constant of integration stems from the first time you integrate the equation -> +C1 and C1 is any reals number.
When you now de-logarithmize it gets C=exp(C1) and now C only can be positive!!!
But because the integration of 1/x actually is ln (|x|) (note the absolute value), at the end C can be chosen any real number.
BTW, Prime can solve the simple ODE in one go:
The sign of the constant C does not matter. I could as well have substituted _z (thats the name of the variable generated by Prime originally) by -C to get the solution you highlighted.
BTW, even though it doesn't mean anything, the solution of Wolfram Alpha also uses the same sign convention
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here the integration of the simple ODE y'=-y in more detail.
Many people don't do it that way, though, because they (hopefully) know that at the end the constant is allowed to be any sign.
But this actually is only true because of the absolute value you get when you integrate 1/y.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the very kind explanation, I was sure of it that the error was on my side, but the teacher insisted that mathcad solved it wrong, which got me endlessly confused. She has a real gripe against using tech in math (eventhough it is mandatory), so she was probably ignoring my question. I'm thinking of showing her this.
Thanks again though.
Kind regards
Amgad