Happy n! day

[ValeryOchkov]

Do you know why 0!=1?

99% persons does (do?) not know it.

[Loris]

By definition?

[MichaelH]

I think it has to do with the gamma(n) function, which looks like (n-1)! for integers.

Then gamma(1) can be shown to be 1 theoretically, so I'm guessing that by convention 0! is also 1 for consistency.

[RichardJ]

It's defined that way, although for good reason. An explanation is here: http://mathforum.org/library/drmath/view/57128.html

[ValeryOchkov]

We can CALCULATE that 0!=1

[hilbert]

n!=n*(n-1)!

if n=1 then 1!=1*(0!) therefore 1!=0!=1

[RichardJ]

Patrick Maxfield wrote:

n!=n*(n-1)!

if n=1 then 1!=1*(0!) therefore 1!=0!=1

That's not a valid proof. n!=n*(n-1)! except when n=1, because then n-1=0, and until 0! is defined to be something you don't have a value for it. If we define 0! to be 1 then the expressoin is true for n=1, but then we already know what 0! is, becase we defined it that way.

[hilbert]

My post gives a reason why 0! should be defined to be equal to 1, that reason being "to maintain algebraic consistency".

Your comment does not give a reason why you defined 0! to be one, rather, you just assert that you defined it that way.

[RichardJ]

My post gives a reason why 0! should be defined to be equal to 1, that reason being "to maintain algebraic consistency".

You posted the calculation without any explanation, so I assumed you meant it as a proof. So I pointed out why, as a proof, it's not valid.

Your comment does not give a reason why you defined 0! to be one, rather, you just assert that you defined it that way.

I only asserted that the calculation you showed is not valid unless 0! is already defined to be 1. That is true regardless of who defined it that way, and whether it was done for a good reason or a bad one.

I pointed out in my first post that it is defined as 1 for a good reason.

[ValeryOchkov]

5!=1*2*3*4*5=120

4!=5!/5=24

3!=4!/4=6

2!=3!/3=2

1!=2!/2=1

0!=1!/1=1

-1!=0!/0=...

[RichardJ]

A variation of a commonly quoted "proof". However, it's not valid either. See http://wiki.answers.com/Q/Why_is_zero_factorial_equal_to_one

Basically, the defintion of a factorial is

n!=n(n-1)(n-2)......1

You get your "proof" by dividing both sides by n, so that the LHS is n!/n and RHS is (n-1)! However, if n is equal to 1 then the only factor on the RHS of the original defintion is n (i.e. 1). The factor (n-1) exists only if n is at least equal to 2.

[ValeryOchkov]

Recursion*

or without programming:

*) See Recursion

[MichaelH]

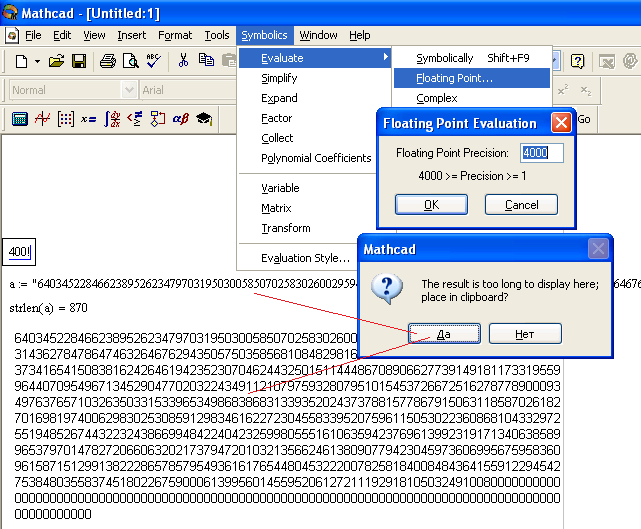
Here is a little program that calculates n! up to 400 factorial and shows all the digits.

In case you were wondering, here is 400! in all its glory. (Start reading the digits from the bottom up)

64 034 522 846 623 895 262 347 970 319

503 005 850 702 583 026 002 959 458 684

445 942 802 397 169 186 831 436 278 478

647 463 264 676 294 350 575 035 856 810

848 298 162 883 517 435 228 961 988 646

802 997 937 341 654 150 838 162 426 461

942 352 307 046 244 325 015 114 448 670

890 662 773 914 918 117 331 955 996 440

709 549 671 345 290 477 020 322 434 911

210 797 593 280 795 101 545 372 667 251

627 877 890 009 349 763 765 710 326 350

331 533 965 349 868 386 831 339 352 024

373 788 157 786 791 506 311 858 702 618

270 169 819 740 062 983 025 308 591 298

346 162 272 304 558 339 520 759 611 505

302 236 086 810 433 297 255 194 852 674

432 232 438 669 948 422 404 232 599 805

551 610 635 942 376 961 399 231 917 134

063 858 996 537 970 147 827 206 606 320

217 379 472 010 321 356 624 613 809 077

942 304 597 360 699 567 595 836 096 158

715 129 913 822 286 578 579 549 361 617

654 480 453 222 007 825 818 400 848 436

415 591 229 454 275 384 803 558 374 518

022 675 900 061 399 560 145 595 206 127

211 192 918 105 032 491 008 000 000 000

000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000

[ValeryOchkov]

400! in Mathcad 11:

[ViktorKorobov]

17236 and 134474... This is the magic number in Mathcad15?

[MichaelH]

The article in Wikipedia claims that 0! is 1 for consistency with "empty set" convention in mathematics.

http://en.wikipedia.org/wiki/Factorial

I take that to mean that there is no definitive proof; rather it's a matter of practice.