Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Help! Odesolve and Pdesolve questions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Help! Odesolve and Pdesolve questions
I am new to using the Odesolve and Pdesolve functions; see attached Mathcad 15 file.
- Okay, I figured out that the independent variable of Odesolver must be x and cannot be another variable like t.
- I also discovered that the x range cannot be defined as a 2 row 1 column vector even though the Mathcad 11 manual indicates that is possible. This must have changed. However, it is possible in the Pdesolver.
- Okay, I discovered that the independent variable must be an integer in integer steps, so I cannot define times less than 1.
- As shown in the attached Mathcad 15 file, I can solve a simpler form of the transmission line equations for a buried line where V is assumed constant over the line with the Odesolver. I am able to include time (i.e. x) varying resistance and inductance of the buried line with a time varying driver E(x).

- In the solution to this ODE as shown in the attached, how do I determine the actual values of x (i.e., the actual time values).
- Now, when I try to solve the complete buried transmission line equations with the Pdesolver, I get the error that V is undefined as shown in the attached. Why?
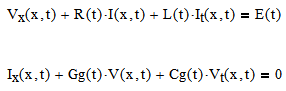 with R(t) and L(t) the same as in the above example, and Gg(t), and Cg(t) similarly defined
with R(t) and L(t) the same as in the above example, and Gg(t), and Cg(t) similarly defined - And, as in 5 above, how do I determine the actual values of t if I ever get this solved?
Thanks much for any help,
Reg Curry
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Reg Curry,
The partial derivatives of the unknown functions are not written correctly.

with their related initial and boundary conditions ....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You also have to use literal indices (V.x) and not vector indices (V[x) as you did. Probably that was the reason you ended up with the multiplications FM pointed you to.
Furthermore you have too many initial conditions - you will have to delete E(0)=0 as you don't solve for E anyway.
After correcting all of the above it works, but after a while we get the error "Repeated singularity problems encountered". Maybe you'll have to recheck your equations and conditions.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks much guys. Both F.M. and Werner are correct. Not only do I have only 3 neurons left working, my eyesight is failing at 74. I accidentally first used vector indices and then just deleted them and inserted literal indices. Apparently that caused the multiplication problem. I never noticed it.
F.M--the equations I am trying to solve have a uniform electric field over the entire line, that is the reason for the syntax of the equations.
Werner--after making the corrections you and F.M. noted, I get the same singularity problem you note. At present, I am not sure where the singularity problems arise. I have solved the same equations using explicit differencing in Mathcad with no problem. I need to do some more thinking on this.
Thanks again guys. Is there a way to give both of you the credit for the correct answer to my original question?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the clarity about the uniform electric field along the line, I thought it was excited at one extreme. Even for me, the program does not work. Let's see if Werner succeeds.
I would still wait to see if there are others, in the community, who want to contribute, with their help and experience, in dealing with the problem.
Greetings
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The solve block apparently does not like the values of Gg(t). If I fix that at 5x10^-2, it works unless I choose a ground conductivity greater that 10^-3. So, I clearly don't understand the solution space for these two PDEs. Perhaps I need to stick with explicit finite difference. To solve this problem with that method takes over 30 minutes, but it does work. I have attached a pdf of that Mathcad sheet after evaluation is complete.

If Ground conductivity = 10^-2
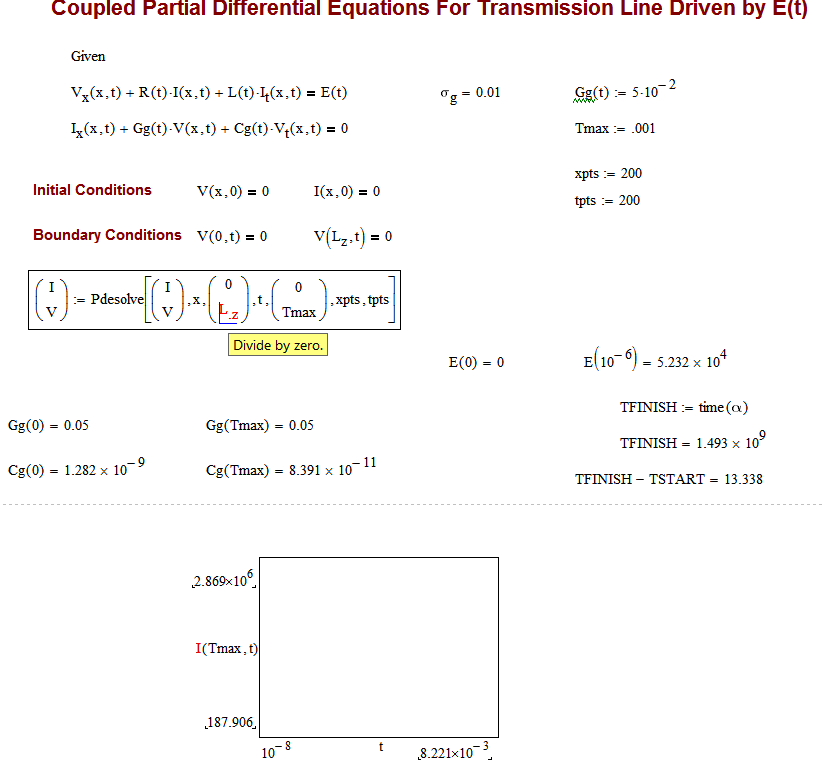
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I wasn't able to make it working, too.
I played around with different (silly) functions for E(t) and it worked.
So maybe we run into numerical inaccuracies or the like. Not sure, though.
For whatever it may be worth I attach a screenshot of one of the tries. With this one I also had to lower the value of xpoints to avoid the error.
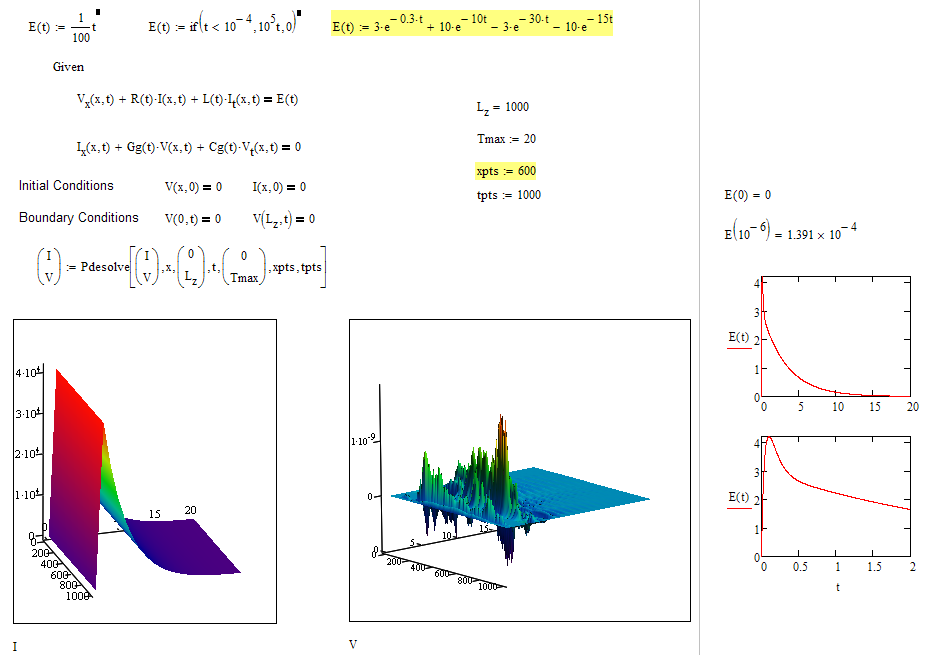
BTW, I am surprised that you plot I(Tmax,t), after all, Tmax is a t-value, not an x-value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The I(Tmax,t) was a mistake. I intended to write I(Lz,t). I told you I am 74 with only 3 neurons left and poor eyesight. LOL
Nevertheless, thanks again to you and F.M. You answered my basic question on my incorrect syntax for pdesolve. I was just hoping for a faster method than explicit finite differencing.
Take care,
Reg





