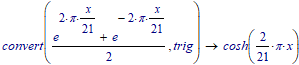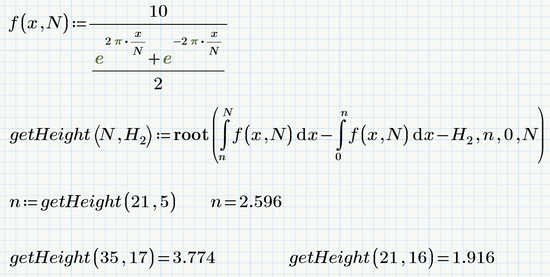Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Help solving integral equilibrium problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Help solving integral equilibrium problem
Hello,
I have a formula which defines water-pressure on a surface depending on depth and wavelength.
To find the total force I have defined an integral.
I want to find the depth beneath the water level where the resultant is located.
I can do this manually by guessing values but I would like the program to solve this for me.
The only variable here is the depth for what I'm understanding by looking at my functions.
Can someone help me understand what I'm missing in the attached calculation?
Regards
/Tobias
Solved! Go to Solution.
- Labels:
-
Civil_Engineering
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
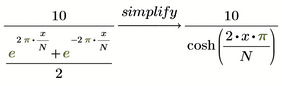
Your expression with exponentials simplifies to the cosh() function.
With that:
And a Solve block is not necessary, for a simple 1 variable solution you can use the root function.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1. Please upload here your Mathcad Prime worksheet.
2. What version of Mathcad Prime are you using?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your expression with exponentials simplifies to the cosh() function.
With that:
And a Solve block is not necessary, for a simple 1 variable solution you can use the root function.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
Ah this was the simplified solution I needed.
Thanks for the help!
I had problems writing out the cosh function which is why I wrote it in terms of exponentials.
But now I know how it's done! 🙂
Was not aware of the root-function, thanks alot!
Regards
/Tobias
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I second what Luc already wrote concerning simplifying the integrand
and the use of the "root" function.
I just wanted to answer your question about
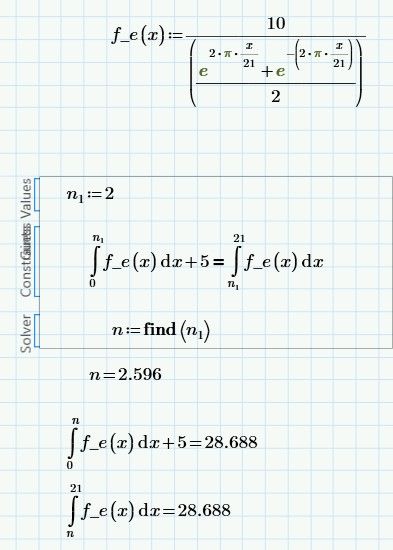
Can someone help me understand what I'm missing in the attached calculation?
The problem is because you introduced three intermediate variables H, H1 and H2 in your solve block, which initially are unknown and undefined.
Because of that you would have to solve for these variables as well and provide guess values, even though you actually are not interested in their final value. After all you have four equations in your solve block, so solving for four unknowns may work well (and it actually does):
But again, I won't suggest doing so.
I am not sure if you maybe need the very same calculation multiple times and with different values for total height N (21) and height H2 (5).
If so, you may consider using a little function with these values as argument. My suggestion uses the "root" function by providing a range (0 to N) and so is self-contained and needs no external guess values:
Not sure about the meaning of the "10". You may add it as a third argument to the function if necessary