Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How IFFT works?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How IFFT works?
Hi,
I'm trying to understand how the IFFT works.
The most difficult thing to be understood by me is the reason why, having 2049 complex samples (p0) I get as a result (4096) real numbers.
The complex samples are not generated by me, are the result of an algorithm written by others.
So I try to understand if there is something special in those samples.
I tried to compare the result with what I get with Wolfram Mathematica (sorry about that):
InverseFourier[p0, FourierParameters -> {1, -1}];
and I get (2049) complex numbers. To get something similar in shape I need to take the real part of those numbers.
Beside that the result of the IFFT is 2048 (magic number!) larger than the result of the InverseFourier.
Can anyone explain to me the reason of those "mysteries"?
Thanks
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Are you using Prime or real (legacy) Mathcad (version 15,14, ...)?
In Primes help you won't find much information about "IFFT" because PTC has replaced it by "idft" and considers "IFFT" as deprecated.
Discrete Fourier Transform of Data
Maybe the original help (from MC15) can be of information to you - at least it explains The "magic number" ( a power of 2)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I'm using Mathcad 15. I was aware of that help, thank you.
My main concern is: how special is that complex function that its Inverse Fourier is real? Better: is IFFT really an Inverse Fourier?
Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I remember questions about ifft and IFFT here in the forum in the past and a comparison with the results of other programs like MatLab.
I think that Tom Gutman answered in a quite old thread in more detail about it. You should be able to find those threads using the search function.
EDIT: Just tried and wasn't able to find that thread I had in my mind. So something is not working - either the search function here or my memory 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
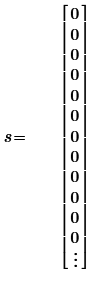

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
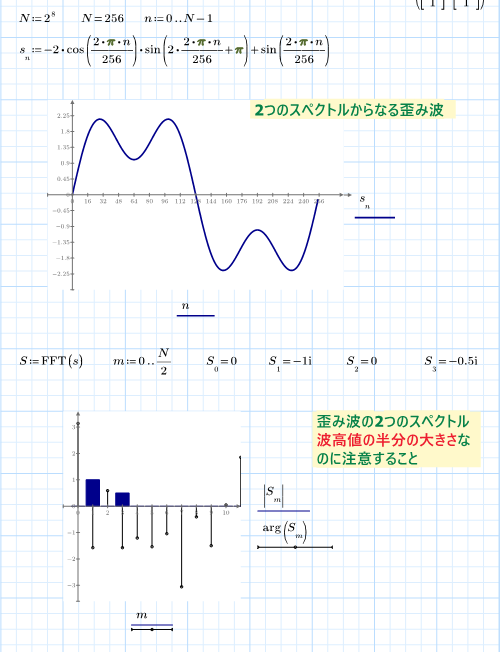
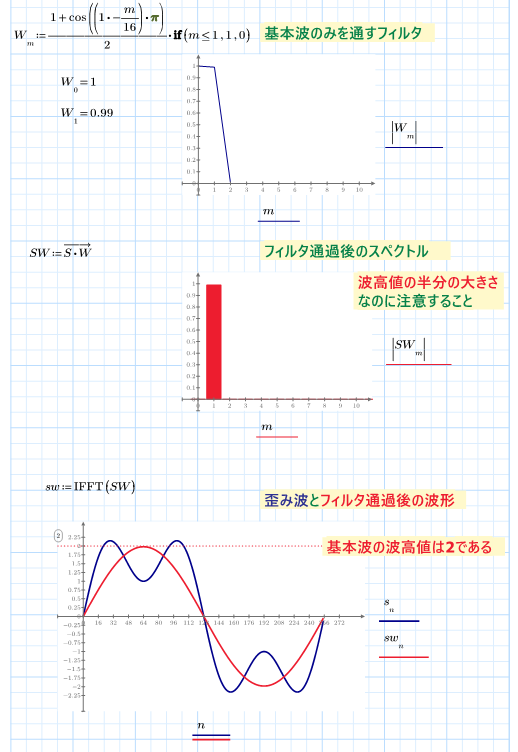
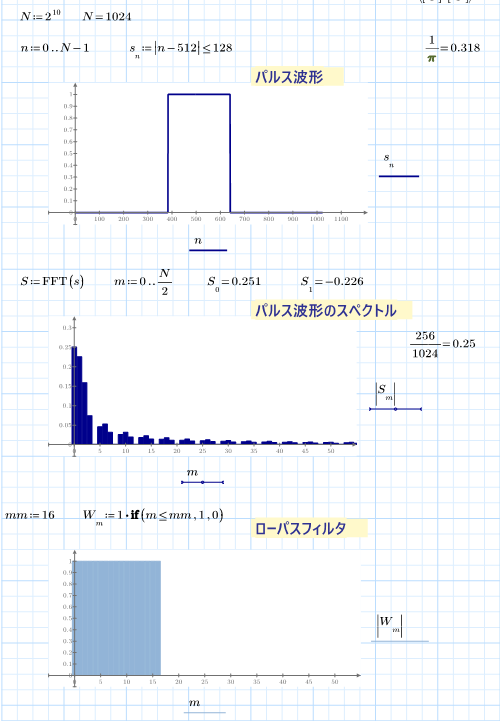
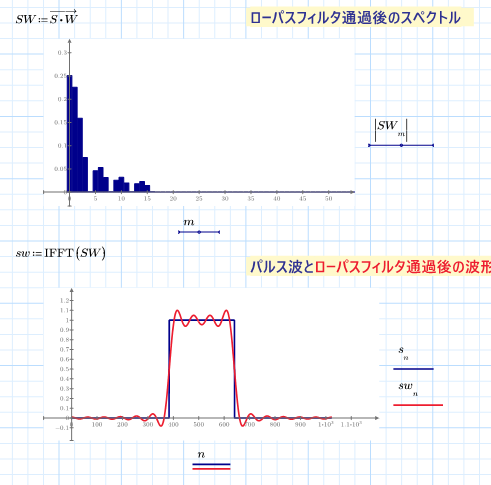
You may be interested in this work of mine which you find attached in pdf format, created by me with MATHCAD 15. Up to page: 71 very useful programs are shown, then the functions that generate the impulses and from page 72 the periodic functions with the spectra and its reconstruction with Shannon.