srqt(a)*srqt(b) as sqrt(ab); sqrt(a-1)*sqrt(a+1) as sqrt(a^2-1). Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How tell Mathcad to simlify square roots?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How tell Mathcad to simlify square roots?
I want to simplifying radicals in Mathcad. I have expression with product of radicals and want use this rule of transformation: The product of the square roots of each factor is equal to the square root of a product How I can do it? For example, Comment I have complex expression that can simplify by use last transformation, but Mathcad don't view how simplify it, how explain Mathcad use above rule? |
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
- Tags:
- simplify
- square_root
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What Luc has shown was the way Mathcad 11 did it using Maple for symbolics.
In Mathcad 15 and in Prime the symbolics are done by muPad (Maple usually was far superior) and muPad handles some things differently. While Maple usually replaced roots by rational exponents, muPad uses roots in its results, too (which generally can, but must not be seen as improvement).
As Luc already said, the rule you mention only applies if the radicand is real and positive and thats exactly what we have to tell muPad using the "assume" command:

Nevertheless someone has to explain this:

Not sure why the first two lines work, as we could have either an expression like sqrt(0.5-1) which is not defined (if we consider demain real) or we are in domain complex, where the simplification rule does not apply.
Obviously only the result is viewed where he radicand is positive as long as a is greater than or equal 1.
Mathcads symolics can be quite tricky and ever so often, especially given more complex expressions, we find no way to talk Mathcad/muPad to use the simplification we see with naked eye but mupad refuses to apply. Symbolics sure is not the strongest part of Mathcad.
Werner
EDIT: Concerning the simplification rule: One (and only one) of the roots involved can have a negative radicand and the rule still applies even in complex.
So in this example
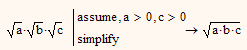
its not necessary that b is real and positive, too. Thats the reason the above examples which had confused me did worked OK.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your statement:
The product of the square roots of each factor is equal to the square root of a product
is true when each factor is at or above 0.
That is one of the reasons why it is hard to force Mathcad to simplify as you want it.

Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks! I have some progress, but substitute work only when I write original expression under root, it is not simple.
1. My decision make not readable, I have some different part this same transition in radicals . I's better to write as you:
"substitute, sqrt(a)*sqrt(b)=sqrt(a*b)"
2. What I can do when I don't view with naked eye this transition to simplify expression?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What Luc has shown was the way Mathcad 11 did it using Maple for symbolics.
In Mathcad 15 and in Prime the symbolics are done by muPad (Maple usually was far superior) and muPad handles some things differently. While Maple usually replaced roots by rational exponents, muPad uses roots in its results, too (which generally can, but must not be seen as improvement).
As Luc already said, the rule you mention only applies if the radicand is real and positive and thats exactly what we have to tell muPad using the "assume" command:

Nevertheless someone has to explain this:

Not sure why the first two lines work, as we could have either an expression like sqrt(0.5-1) which is not defined (if we consider demain real) or we are in domain complex, where the simplification rule does not apply.
Obviously only the result is viewed where he radicand is positive as long as a is greater than or equal 1.
Mathcads symolics can be quite tricky and ever so often, especially given more complex expressions, we find no way to talk Mathcad/muPad to use the simplification we see with naked eye but mupad refuses to apply. Symbolics sure is not the strongest part of Mathcad.
Werner
EDIT: Concerning the simplification rule: One (and only one) of the roots involved can have a negative radicand and the rule still applies even in complex.
So in this example
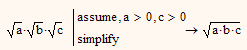
its not necessary that b is real and positive, too. Thats the reason the above examples which had confused me did worked OK.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!





