Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to derive the expressions of the variables in the linear equations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to derive the expressions of the variables in the linear equations
Hi all, if I have the three variables in three equations, would you advise me how to use mathcad to express the derived expression of the variables?
I have three unknown variables x,y,z, and three pre-defined values a, b and c.
If I have
x+y+z=a
x+2y+3z=b
x+3y+4z=c
would you teach me how can I use mathcad to express x, y, z as the expressions of a, b and c, instead of assigned the numbers to a,b and c then solve x,y,z as the fixed numbers? Thank you!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe something like this;
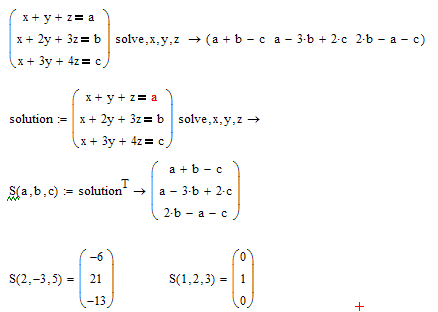
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Werner, another question for a more complicated case. In the following case
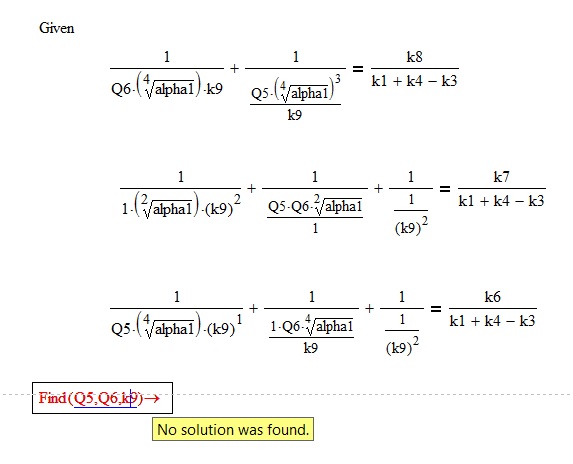
Q5, Q6 and k9 are variables, and all other parameters are not defined in previous text. How can I use Mathcad to derive the expressions of Q5, Q6 and k9 by alpha1, k1,k3,k4, k6, k7 and k8?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should always attach your worksheet as most people are like me not willing to retype the whole thing to be able to play around with the problem.
I am not sure if MC can be talked into providing a solution.
Maybe it helps, if you assure all other variables/constants are real numbers, or maybe even positive numbers - you du this by using the "assume" statement.
Mathcad has to consider all possible conditions, some of which we possibly won't even think of, if we where to solve this by hand.
It may also be, that there is no closed analytic solution available in which case the symbolics can only fail.
Maybe the symbolic solve command is more helpful than a symbolically evaluated solve block.
You just have to play around with the problems and try different things.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner, thank you for your advise. Sorry to cause the inconvenience to you. I have attached the source code of my question, and would you help me again in finding what is the problem of my code?
This time my questions is as this picture

Thank you so much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think it's possible to find a symbolic solution for that system of equations (by which I mean not just that Mathcad will not find one, but rather that it's not possible). Just looking at k9, some terms have k9^2 in the numerator, some have k9 in the numerator, some have k9^2 in the denominator, some have k9 in the denominator, and some do not have k9 at all. That means your equations are fourth order polynomials in k9, and in general there is no symbolic solution in such a case (the symbolic solution for second order, or quadratic, is well known; the symbolic solution for third order, or cubic, is very big and ugly, but it exists; there is no known solution for fourth order).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Richard!





