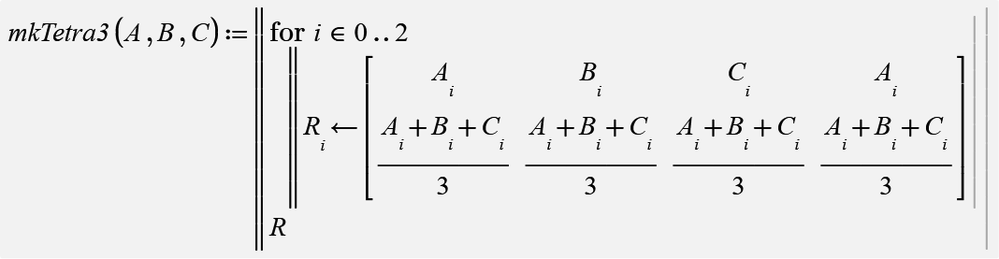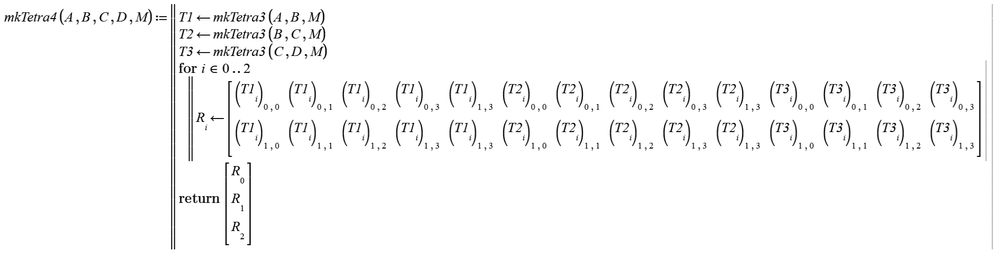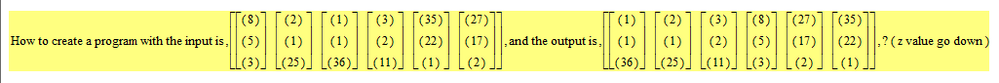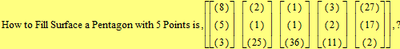Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to "Fill Surface" a Hexagon in 3-D ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
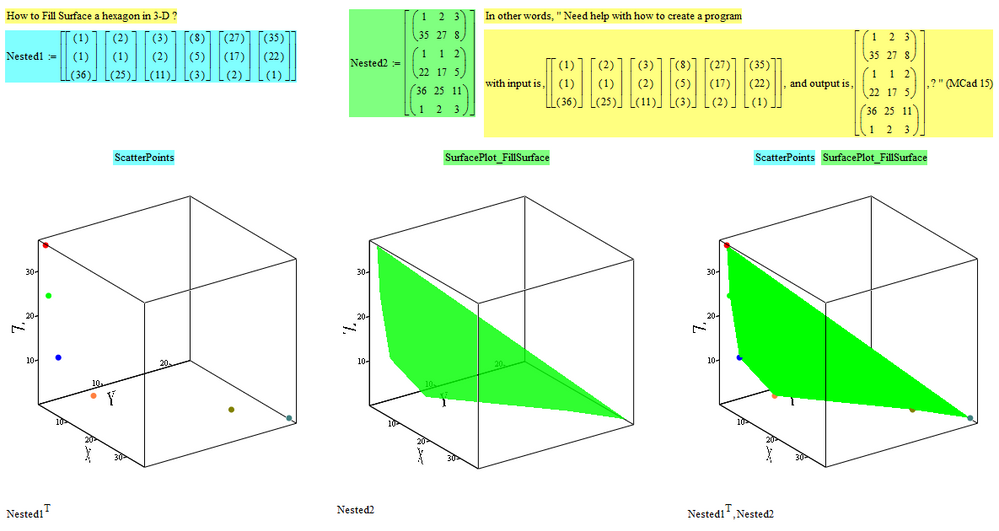
How to "Fill Surface" a Hexagon in 3-D ?
Hello, Everyone.
From the following :
Thanks in advance for your time and help.
Best Regards.
Loi.
Solved! Go to Solution.
- Labels:
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To close this thread (for me), here is a function to implement #4 in my list above. #1 - #3 will be up to you ore somebody else 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The attached should do the job. Works for exactly six points only and the order the points are given is important. So its very specialized and thats the reason I did not made any attempts to make the program ORIGIN independent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, Everyone again.
From the following:
And if we get the input with random order of the points, and how to sort them for the program function always is true. And my belief is going to have a program function apply for any polygon, any order of the points and sorting say: Pentagon, Seven-Edge . . .
Best Regards
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And my belief is going to have a program function apply for any polygon, any order of the points and sorting say: Pentagon,
If you change the order, you get a different polygon!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yeah ! you're right. A pentagon must be convex, and sorting that five points in accordance with certain rule, and Fill Surface !
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Everyone, again.
From related query as the following :
How to create that program function ?
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Like this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Clear and neat answer !, Werner. 🙂🙂🙂
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
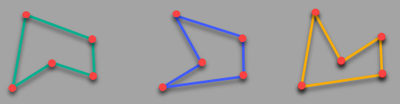
For generalizing the problem:
How to Fill Surface a (convex) Pentagon ?
Best, Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to Fill Surface a (convex) Pentagon ?
Probably like outlined here: Solved: Re: Rotate a quadrilateral in 3-D ? - PTC Community
But you will have to
1) Check, if all points are in the same plane and at least one is not on the same line as the others - Otherwise: error
2) Check if its possible to form a convex polygon using the given points - Otherwise: error OR you find a decent method how to fill a concave polygon, too.
3) If a convex polygon is possible, you have to find a way to arrange the order of the points so they form the convex polygon in that order
4) Now you can follow with the method outlined in the thread mentioned above, creating for example the structure where all points from #3 to #n-2 are connected with point #1 (last picture in that thread).
Sure a task for some cold winter days ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To close this thread (for me), here is a function to implement #4 in my list above. #1 - #3 will be up to you ore somebody else 😉