Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to search a Matrix for a number bounded by another number?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to search a Matrix for a number bounded by another number?
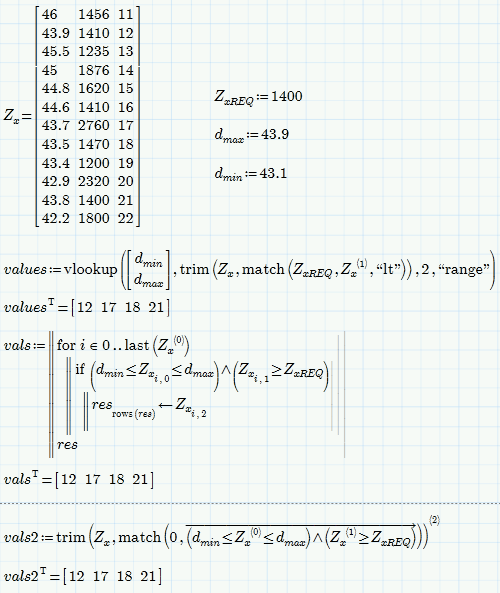
In the attached Prime worksheet is it possible to create a function that can search the second row of the matrix for the a number closest but higher than ZxREQ while also making sure that it's corresponding value in the first row is between dmax and din? The issue I'm having is how do you search in a particular row in a matrix?
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Changed the sample data
Simplified the first method.
Changed all methods to use <= rsp. >=
Added a third, tricky method
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From the file you posted it looks like you are searching a value in the second column, not in the second row.
BTW, what should the outpit of that function be? A list(vector) of indices as Match would return? The first value of the second column which fits? A vector of all values of the second column which fit? The samllest value in the second column that fits? ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're right, I did mean the second column.
The function would output the corresponding value in a third column which I will add.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Then you should setup a sheet with complete data!
So the value in the second column should be > (or >= ) ZxREQ?
The value in the first column should be between d.min and d,max. Usually this would exclude values equal to d.min or dmax. Is that correct?
The output cant be just a value but rather a vector of corresponding values from the third column as it may not be only a single value which fulfills tghe conditions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here are two different ways of achieving what you demanded so far (no error checking implemented so far):
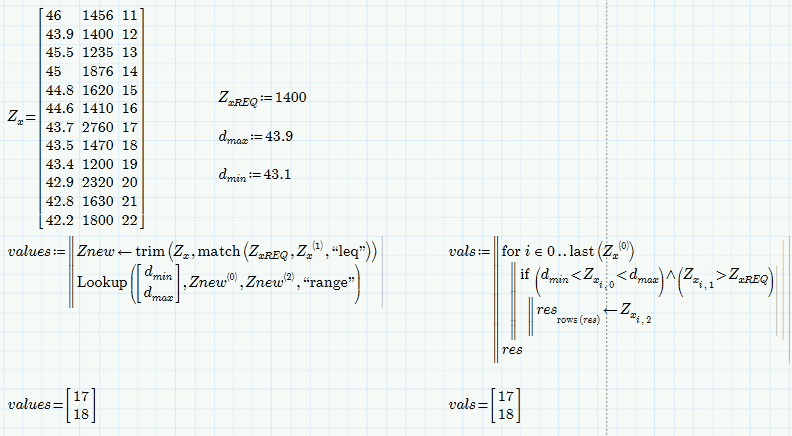
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Changed the sample data
Simplified the first method.
Changed all methods to use <= rsp. >=
Added a third, tricky method

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your help Werner, is it possible to create a vlookup that looks in a specified column, not just the first column?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Daniel Sochor wrote:
Thank you for your help Werner, is it possible to create a vlookup that looks in a specified column, not just the first column?
Sure, look at the last two approaches I posted and change the 0 index to whatever column you want.
When you try to develop a generic new routine I guess the most labourious part would be to implement the various modifiers ("range", "neq" ,....).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is a very elegant solution. Can it only return integers or can it be modified to return text in parenthesis?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Daniel Sochor wrote:
This is a very elegant solution. Can it only return integers or can it be modified to return text in parenthesis?
I am not sure what you mean?
If the values in the column vlookup should return are strings, you will get a string as result.
If you are happy with "eq" and don't need the other modifiers, here is a vLookup as you requested:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Forgive me, I made a mistake in applying your work and assumed the error was due to the first column of data not being integers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Daniel Sochor wrote:
Forgive me, I made a mistake in applying your work and assumed the error was due to the first column of data not being integers.
I guess the error was because you had set ORIGIN to 1 and my routines assume the default ORIGIN=0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In your third tricky example, what is the 0 doing in the match function? Is it looking for a match of 0 in the trimmed columns of Zx?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Daniel Sochor wrote:
In your third tricky example, what is the 0 doing in the match function? Is it looking for a match of 0 in the trimmed columns of Zx?
No, match() looks for zeros but not in the trimmed matrix Zx. As usual in math expressions are evaluated from inside to out, so match() does not know anything about trim(), which is applied later.
The vectorized boolean expression, the comparisons combined with AND, returns a vector consisting of 0's and 1's. 0 means FALSE and 1 means TRUE (actually any number unequal to zero is considered TRUE in Mathcad). Vectorization is necessary as we cannot compare a vector with a scalar and so we would get an error.

We are interested in those values of matrix Zx, column 2, where we get a 1 in the above vector. But as Mathcad does not offer a counterpart to trim (lets say keep()) we look for the zeros.We use match() to get the indices/the positions of all zeros - the index numbers of the rows we don't want to keep. So if you changed ORIGIN from 0 to 1, the zero in match() is a zero you should not change 😉
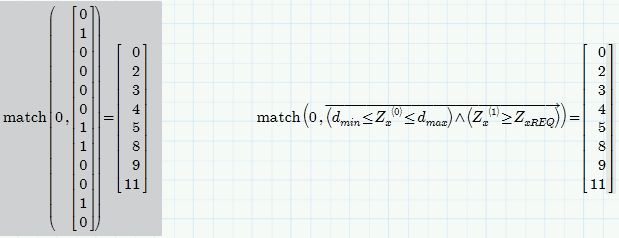
Now we can use this vector of indices as the second argument for trim() to delete all rows in the matrix Zx which do not fulfill your constraints. The result is a multiple column matrix and we select the second column of that matrix to finish and get the values you are interested in.
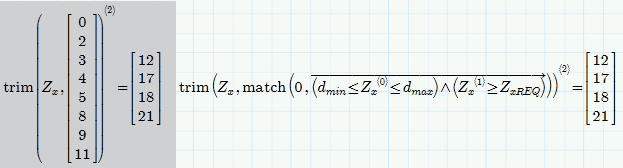
Upon further thinking about this method I guess that
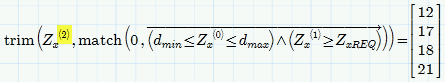
is a bit more efficient and better looking as we select the second column of Zx first and then trim only that column. Maybe just a matter of personal taste.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for this great explanation Werner, I now understand it and am employing it throughout this calculation.
A question about Ceil() that may not be related but maybe I can ask it here;
In the attached MathCAD, the Ceil() function sets 0.375in to variable taRec. However, MathCAD appears to be treating taRec as being above 0.375in. You can see this by moving the taRec=0.375in down slightly (so it's definition supersedes the definition that has the Ceil() function) and the results of your trim & match function change to include angles with a thickness of 3/8in and 7/16in (the seventh column of the matrix is the angle thickness) instead of just 7/16in. Is there something that must be changed in the Ceil() function so the return value stays at 0.375in?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A question about Ceil() that may not be related but maybe I can ask it here;
In the attached MathCAD, the Ceil() function sets 0.375in to variable taRec. However, MathCAD appears to be treating taRec as being above 0.375in.
...which indeed it is (very slightly) because of roundoff errors - presumeably because of unit conversions (m <--> in)

In programming there is a rule that you never should ask that a given float value is exactly equal to another but that you rather should ask if the two value are sufficent near (the absolute value of their difference is smaller than a given small value epsilon like 10^-15).
You can apply a similar workaround in your case
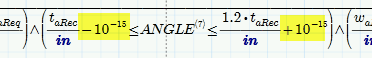
As your values are in steps of 1/16" this should not have any bad side effects, i guess.
There is also another workaround available here, but I am not sure if it will work always in other cases, too:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you again Werner. I have previously been unaware of the concept of a float values. I'll have to look else where in my worksheet for areas where I ask if values are equal to each other and add this 10^+/-15 factor.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Daniel Sochor wrote:
Thank you again Werner. I have previously been unaware of the concept of a float values. I'll have to look else where in my worksheet for areas where I ask if values are equal to each other and add this 10^+/-15 factor.
As an alternative you may try to uncheck "Use exact equality for comparisons and truncation" on the "Calculation" tab of the Worksheet Options.





