Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
I graphed a line in the x y plane that begins at (-9,6) and stops at (2,4). This is because a college algebra book asked to consider the distance FROM P1 (-9,6) TO P2 (2,4). The authors then mention that the "midpoint formula is a bit more complex that i
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I graphed a line in the x y plane that begins at (-9,6) and stops at (2,4). This is because a college algebra book asked to consider the distance FROM P1 (-9,6) TO P2 (2,4). The authors then mention that the "midpoint formula is a bit more complex that i
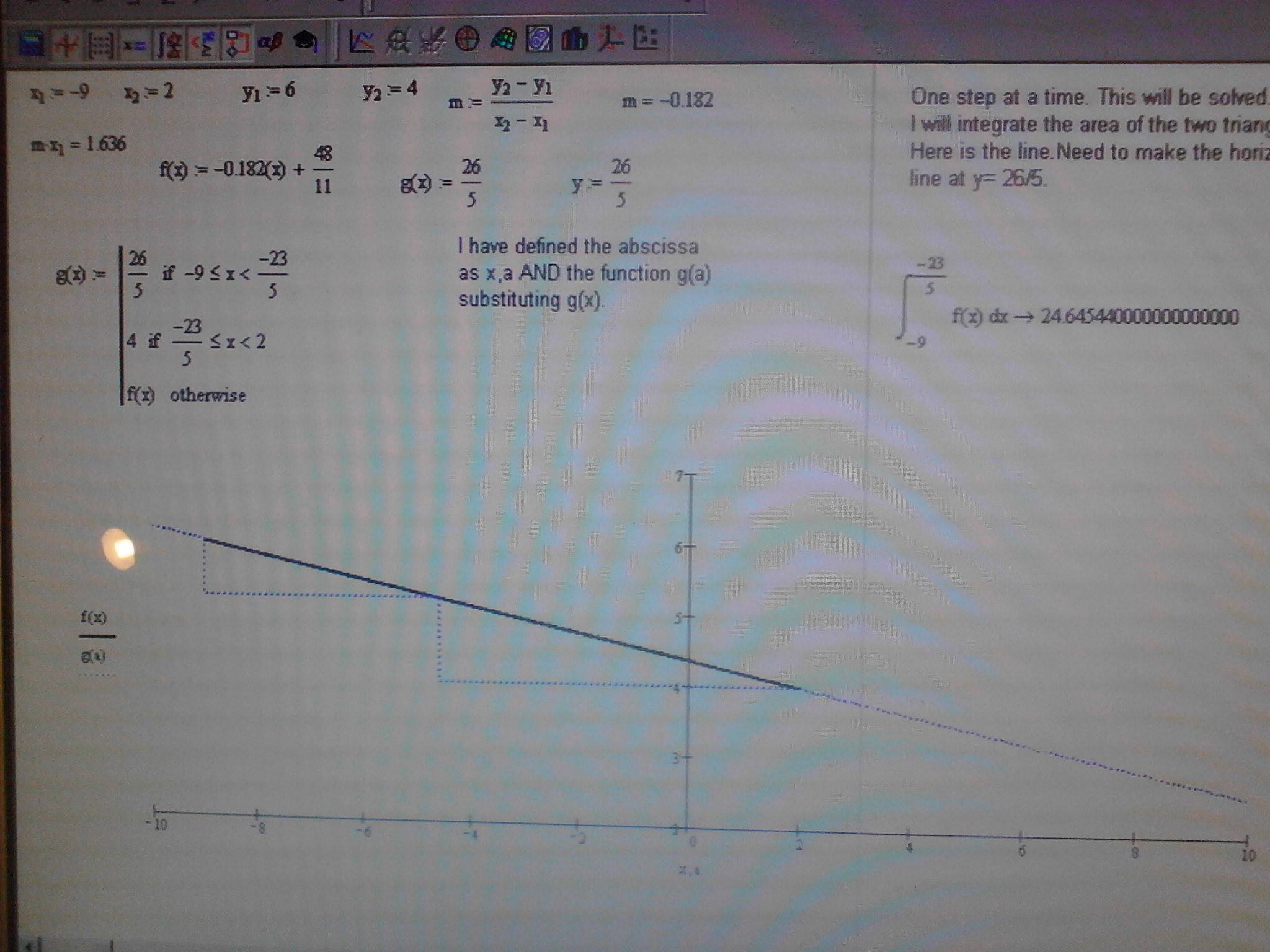
I graphed a line in the x y plane that begins at (-9,6) and stops at (2,4). This is because a college algebra book asked to consider the distance FROM P1 (-9,6) TO P2 (2,4). The authors then mention that the "midpoint formula is a bit more complex that it looks and is actualy a special case of a geometric theorem. Something about the ratios of the distances. Exploring this I then decided to use the mathcad software to create the two right triangles that would be associated with these three points. The point (answer) is P3 (-23/5,26/5). The reason I wanted to create these two right triangles is just to explore my ability to integrate the areas and compare the ratios. And I did it! My graph of the line that starts and stops at P1 and P2 is defined as f(x). To make the two triangles I wrote a program g(x) that uses inequalities and operators. In the placeholder for x and y however the g(x) is stated as g(a) and the x placeholder is x,a. I am not able to post a worksheet. But if anyone can visualize this Algebra problem and plot this scenario I would much appreciate it.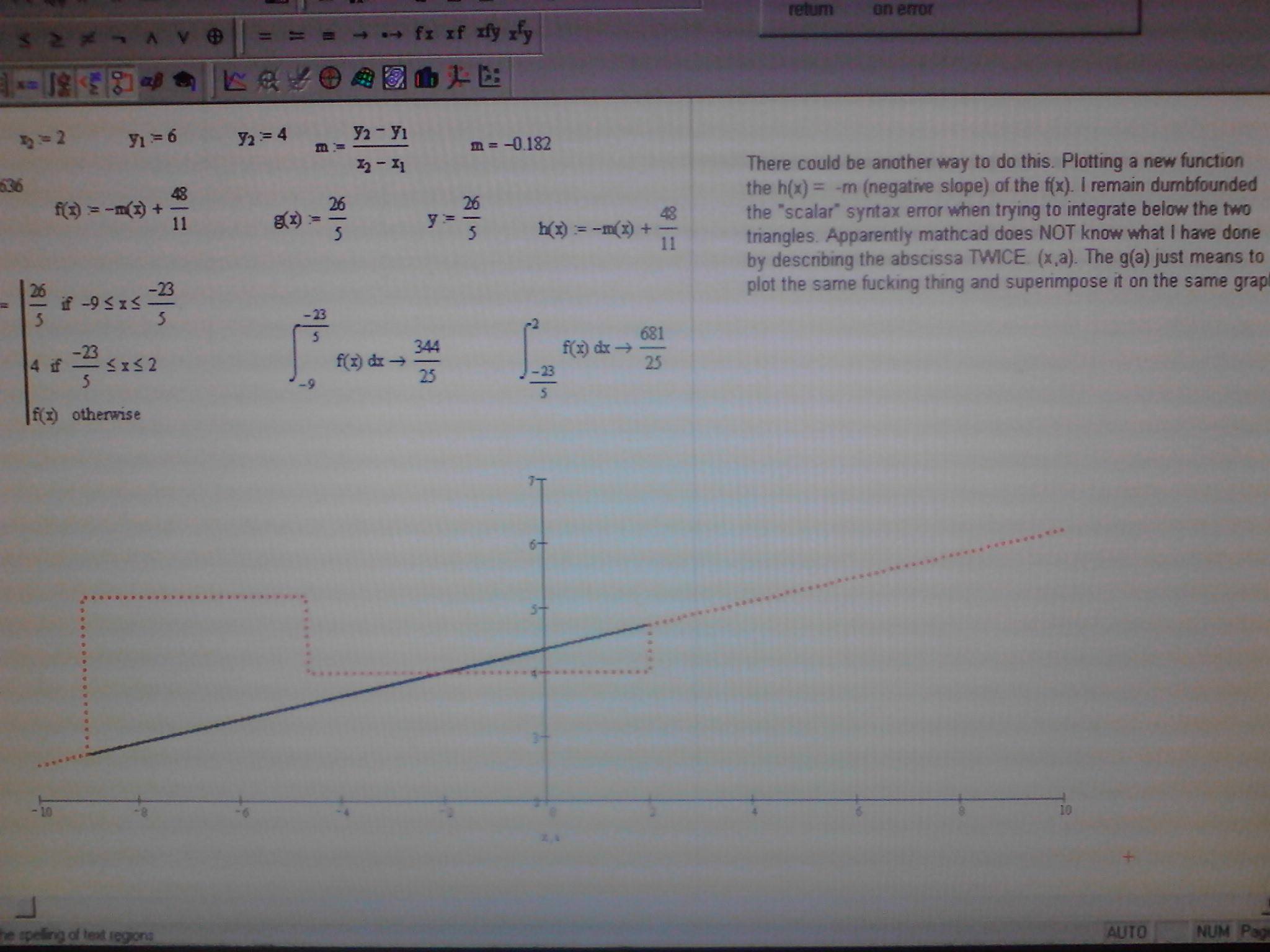
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
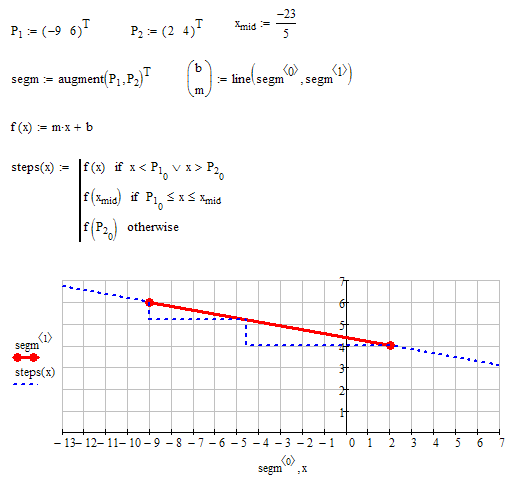
Not sure what exactly you are trying to do, but it looks to me that you typed m(x) instead of m*(x) (or even better simply m*x)
Maybe the attached helps:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you switch to 'advanced editor'

you will find and 'attach' link in the lower right corner.
You will also find that link if you edit your existing entry or answer (one of the options of the 'actions' link in the lower left corner).
You then can attach your worksheet.
(Oh, this forum is such a great place to be ![]() .)
.)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
If you switch to 'advanced editor'
(Oh, this forum is such a great place to be .)
Success!
Luc
Careful,
Your true feelings are peeking out! 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure what exactly you are trying to do, but it looks to me that you typed m(x) instead of m*(x) (or even better simply m*x)
Maybe the attached helps:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner. You have been most helpful over the years. I do not have the ability to post worksheets and only tinker with Mathcad 2000 as a hoby. This will take me quite some time to explore and I am not quite what I am trying to do either . . .but it should be fun.





