Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
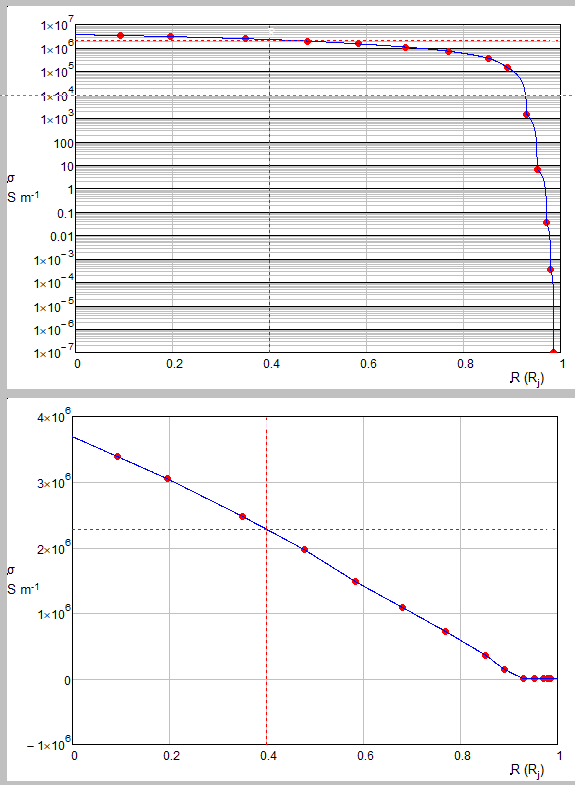
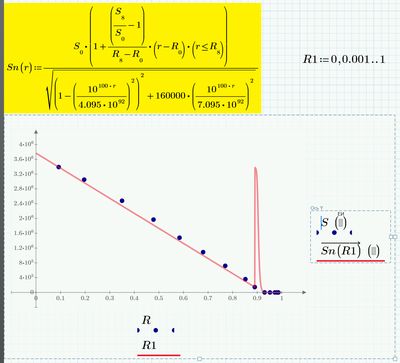
I need a formula for this points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I need a formula for this points
Can you show me one formula for this points? The Mathcad 15 sheet is in attach!
Thank you!
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From the very beginning, I was thinking about this Columbian solution, but I expected a more elegant (smoother, with derivatives!).
PS
What is it one Columbian solution&
They say that Columbus during lunch with Cardinal Mendoza suggested that the present grandees solve a simple problem: put an egg upright on the table. No one could do this, except for Columbus himself - he just broke it from one end. All, interrupting each other, began to resent that so can they. “The difference is, gentlemen, that you could do it, but I actually did it,” the navigator replied.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm limited by lack of version 15.
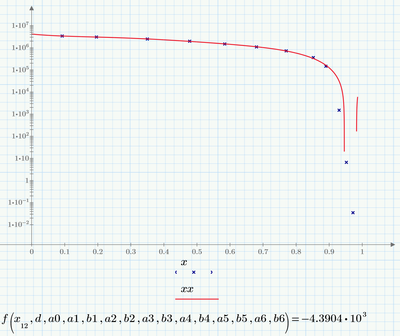
Attached is excel of three fits (curve expert) of digitized data. No good fits, best fit doesn't roll off fast enough, others go negative at high R.
(If you send a cxv file of point values, I can try gain. (You've got my email.)
good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Way back in 1993 or so I had a program, I believe called NFIT. It had several hundred formula built-in that you could cycle through and (usually) find a good fit. I lament that in 2018 I can't seem to find a similar program.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Google curve expert.
Program has many built-ins, and will accept you own special function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I second Curve Expert. I wish Mathcad had that kind of curve fitting capability.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
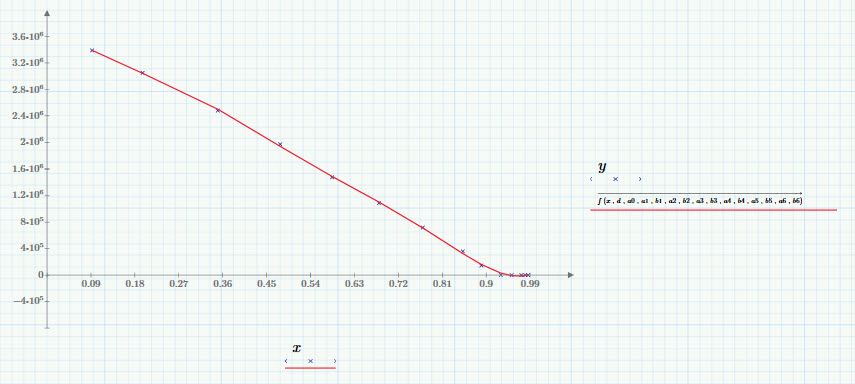
The first points are very nearly a straight line, So curve can be broken into two parts. You could possibly get closer to the last eight points with a different function type besides a line.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks to all!
At our university there was a mathematician who by the type of curve immediately determined the formula f(x,a,b,c…). With guess values for a, b, c... But he, alas, retired!
I need the formula for C++! But at first for Mathcad!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your plot looked a bit like a low pass filter.
So, with a little sleight of hand. . .
In Prime 4 express
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The sheet please!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
I don't have version 15 any longer, stuck with Prime 4.0 express! The last post has your data (thanks SMath) with this solution, the file ochov2.mcdx is a Prime 4.0 file; I'll work on teaching Smath to do this, see if it can write an xmcd file
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
@Fred_Kohlhepp wrote:
Hi Fred! Send please the sheet! Better Mathcad 15!
Attached zip has Smath file and Smath saved to xmcd
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can adjust the break point to fix that--see below:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From the very beginning, I was thinking about this Columbian solution, but I expected a more elegant (smoother, with derivatives!).
PS
What is it one Columbian solution&
They say that Columbus during lunch with Cardinal Mendoza suggested that the present grandees solve a simple problem: put an egg upright on the table. No one could do this, except for Columbus himself - he just broke it from one end. All, interrupting each other, began to resent that so can they. “The difference is, gentlemen, that you could do it, but I actually did it,” the navigator replied.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
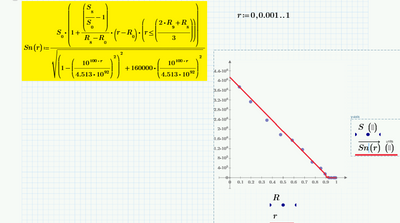
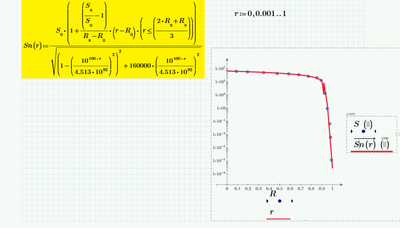
Valery, you showed pics from the linear interpolation in your very first post and you were asked whats wrong with it as its one the easiest ones to be implemented in any programming language. You were asked if you don't like the the "bumps" which it shows in the log plot and are looking for something else for that reason. So I suggested to use linear interpolation of the logarithmized data which is as easy to implement and does not show this undesirable behaviour. You never answered to the questions what you are exactly looking for and why linear interplation would not be acceptable. Fred came up with a very sophisticated solution and even showed you how to adopt it to your needs (you ignored his answer) and now we see that linear interpolation (no one would do it manually in Mathcad) is the solution? I really wonder what the reason for asking here really would have been.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
Valery, you showed pics from the linear interpolation in your very first post
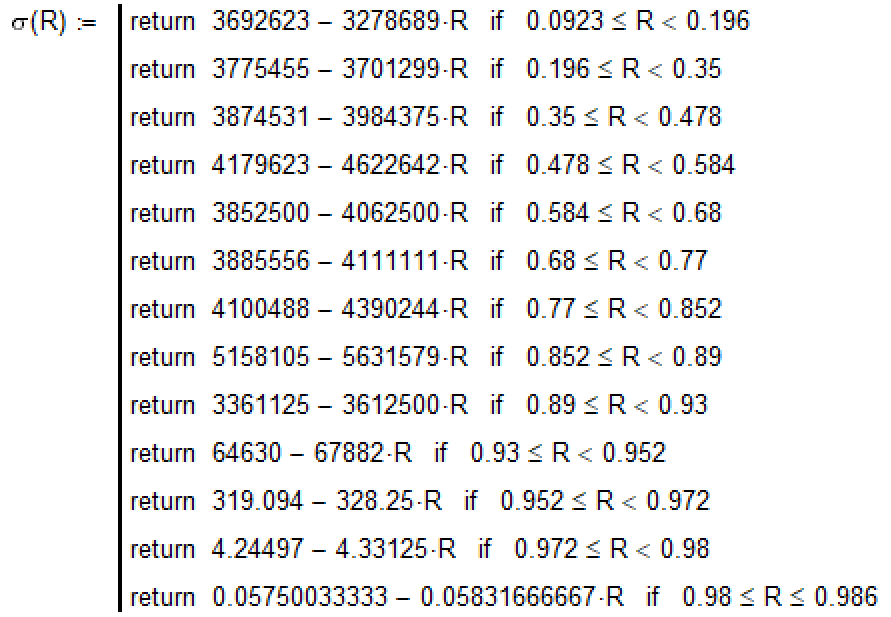
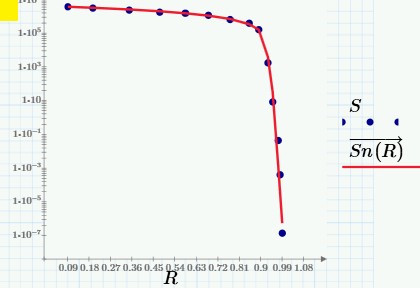
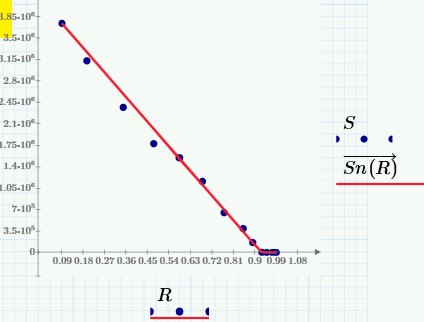
Now I show the formula of this linear interpolation!
I was hoping that with your help I would get a more elegant and short formula. But this did not happen. Thank you all!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Mathcad Web-sheet for calculation and a programs creating:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
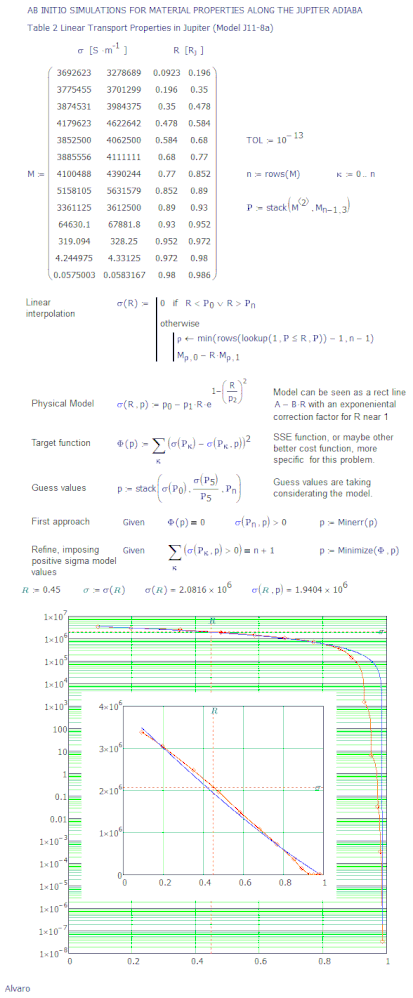
Hi Valery.
I guess that Fred make a great job finding a suitable mathematical model for the data, even have some numerical issues with the tail, where it give negative values, but looks very close to the empirical data.
This other uses a more simple model, and shows how to use minerr for get better guesses values for plug them into a minimize solve block.
Maybe some one can join this procedure with the Fred model, which have more complicated math, but an immediate and well know physical interpretation.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@AlvaroDíaz wrote:
Hi Valery.
I guess that Fred make a great job finding a suitable mathematical model for the data, even have some numerical issues with the tail, where it give negative values, but looks very close to the empirical data.
Best regards.Alvaro.
Thanks for the vote of confidence! But my function form represents a completely different physical event; I only tried to connect the curve shapes of the two events. And not very well1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred.
@Fred_Kohlhepp wrote:
...But my function form represents a completely different physical event; I only tried to connect the curve shapes of the two events.
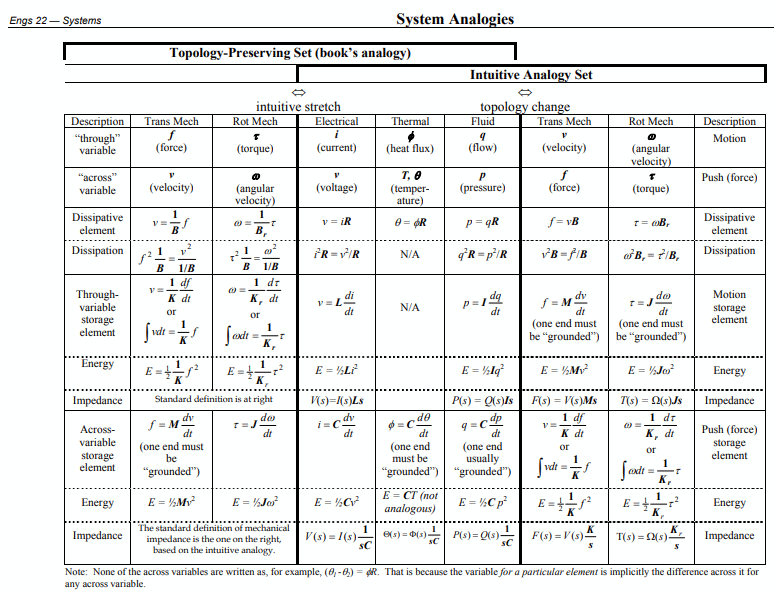
If you recognize the shape of the math of some physical model (for example a thermal model), and know how to interpret it in some other physics field (for example, mechanics), then you can try to found the "thermo-mechanical equivalent" or "analog" interpretation. This applies for electrical, hydraulic, pneumatic and other areas. For example, you can use this table, from http://www.dartmouth.edu/~sullivan/22files/System_analogy_all.pdf
or check the wikipedia article: https://en.wikipedia.org/wiki/Analogical_models
So, your control theory model probably have a thermal equivalent which is an easy interpretation.
@Fred_Kohlhepp wrote:
...And not very well1
I'm not sure about that. Valery's data have an exponential and a lineal part, as is pointed before by Werner. One simple model maybe can contain then exponential errors for some values.
But if the point it's only implement some algorithm in Cpp then I guess that this is the shortest way:
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
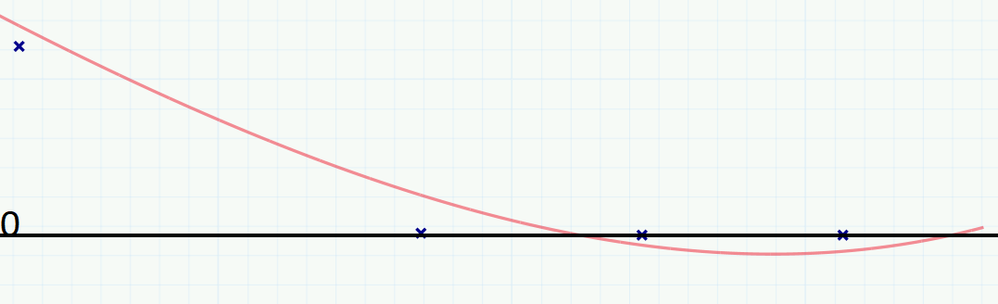
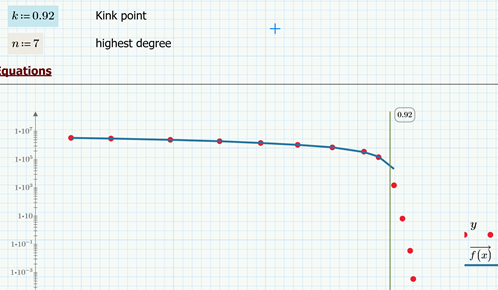
Here's something called Regression Kink Design; seems to be popular in economics. Does a reasonable job. It does undershoot the lowest points if you zoom in. I could only go to 6th order since that's when minerr ran out of variables.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cooooooooooooooooooooooooooooooooooooooooool!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@DJF wrote:
Here's something called Regression Kink Design; seems to be popular in economics. Does a reasonable job. It does undershoot the lowest points if you zoom in. I could only go to 6th order since that's when minerr ran out of variables.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are getting answers, they are just negative answers (the undershoot I mentioned.) So they don't show up on a log chart. As to whether that is acceptable or not depends on what you need for accuracy. If you can be off by 16000 it works fine. If not, back to the drawing board.
I had assumed you were after a single equation, if not I'd agree splines would probably work best.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes - negative!\
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A higher order RKD should help that out some, but I'm not sure how to get there. Someone will probably tell me 15 can do it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@DJF wrote:
A higher order RKD should help that out some, but I'm not sure how to get there. Someone will probably tell me 15 can do it.
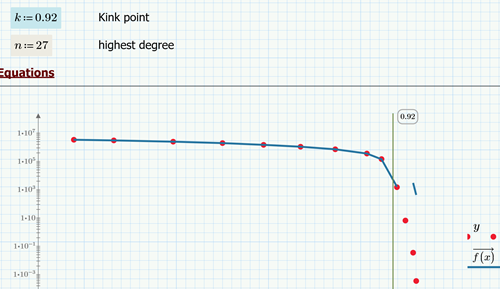
Even Prime can do it, too. But increasing the order doesn't help. After all with n as highest order we have 2*n+2 variables to solve for but still only 14 equations to fulfil.
You may play around with the attached sheet, but I guess this regression will not do whatever Valery has in mind.
Changing the value of the kink point has no big effect, too. Just for fun I added k as an argument of function f and let the solve block optimize k, too, and it came up with k=1.8343.
Worksheet in format P5 attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When k is changed, d just changes to compensate. At least that was my observation.
RKD was basically a way to merge polynomials across a kink point. Is it possible to instead join two exponential curves across a kink point? I think that's what we want since there two straight lines on a log scale.